Screening of molecular crystals by elastic constant calculations

Introducition

The elastic constant tensor is an important quantity that characterizes the elastic behavior of a material. If the components of the elastic constant tensor are known, various mechanical properties can be calculated. One quantity that is important for practical use is the elastic modulus, which indicates the resistance of a material to elastic deformation. For example, artificial structures that are subjected to high mechanical stresses usually require materials with large elastic moduli, typically tens to hundreds of GPa. On the other hand, materials for biocompatible applications are often polymers, which have elastic moduli of several MPa to hundreds of MPa.
Molecular crystals, which exhibit a Young's modulus intermediate between that of hard and soft materials, are important in optoelectronic materials, actuators, and pharmaceutical formulations. However, measurements of the elastic constant tensors have not been performed often due to the difficulty of growing large crystals and the need to measure many components because of their low symmetry.
Therefore, material screening by calculation is effective for the development of practical molecular crystals. Conventionally, theoretical calculations (DFT, HF) have been used to calculate elasticity tensors, but the calculation cost is enormous. Although the recently developed neural network potential (NNP) has a low calculation cost, it has been applied mostly to inorganic materials, and its effectiveness for molecular crystals is unknown.
In this study, we verified the effectiveness of NNP for calculating the elastic constants of molecular crystals [1].

Calculation models and methods

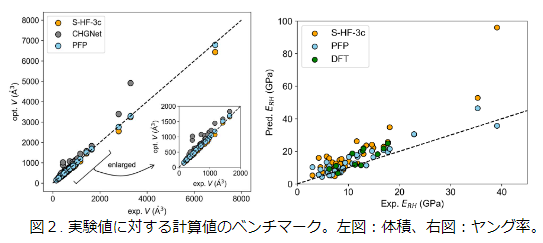
First, we performed a benchmark of NNP. We used the following data from the literature [2]: 123 experimental elasticity tensors for 80 compounds, Hartree–Fock calculations (S-HF-3c) for 44 compounds, and DFT-D calculations for 11 compounds. For the compounds in the S-HF-3c data, we calculated the volumes and elasticity tensors using PFP (v4.0.0) and CHGNet (v0.2.0)[3]. As a result, the accuracy of PFP was higher than that of HF and CHGNet, and was comparable to that of DFT.
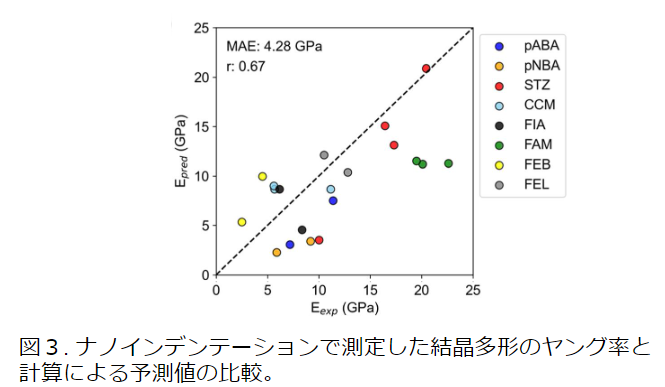
Molecular crystals often have polymorphs with different arrangements, and the difference in the crystal structure affects the elastic constants. If NNP can express the difference in elastic constants due to polymorphism, it will be useful for comparing with experiments. Therefore, we calculated Young's modulus experimental values [4] obtained by nanoindentation for eight polymorphs of compounds using PFP and compared them.

Results and Discussion

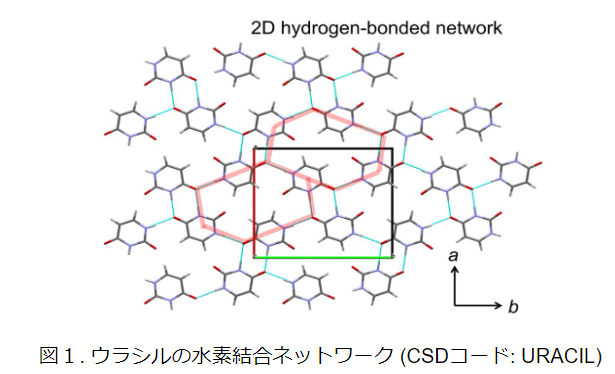
The calculated values of Young's modulus roughly reproduced the experimental trends. For four materials (pABA, pNBA, STZ, and FEB), the trends of the crystal polymorphism in the experiment were reproduced. On the other hand, for the other materials, the differences in polymorphism could not be expressed (FAM, CCM) or the trends were opposite to those in the experiment (FIA, FEL). However, even in the nanoindentation experiment, there is an error depending on the measurement conditions from the true value. Focusing on the relationship between the structure and Young's modulus, it is known that the elastic properties of molecular crystals depend on the hydrogen bonds between molecules. Although the calculated values of PFP did not completely match the experimental values, they reproduced the trends of hydrogen bonds in the crystal structure and Young's modulus, and NNP is considered to be effective in predicting elastic constants.
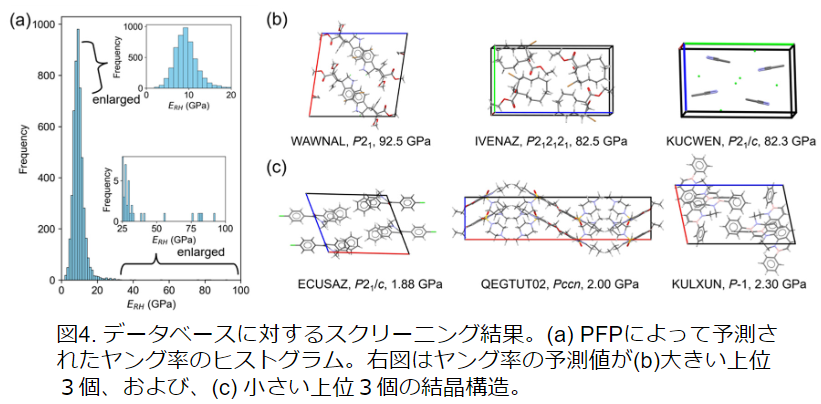
In addition, NNP was used to screen molecular crystals with low and high Young's modulus. 5,000 crystal structures were randomly selected from the Cambridge Structure Database (CSD) and the Young's modulus was calculated. As a result, molecular crystals with a higher Young's modulus than those previously known were obtained. This result indicates that PFP is useful for the exploration of organic crystal materials.

Computational Details

References

[1] T. Taniguchi, CrystEngComm, 2024, 26, 631 [2] PR Spackman et al., Angew. Chem., 2022, 61, e202110716. [3] CHGNet. https://chgnet.lbl.gov/ [4] BP Gabriele et al., CrystEngComm, 2021, 23, 2027–2033.