PostNEMDThermalConductivityFeature

はじめに#

物質の熱の伝わりやすさを表す基本的な物理量、それが熱伝導率です。

熱伝導率を原子シミュレーションで計算する方法として、実時間でのフォノン計算、グリーン-久保公式、非平衡MDなどの方法があります。
matlantis-features では、 reverse non-equilibrium molecular dynamics (rNEMD) 法を提供しています。
非平衡MDトラジェクトリを生成したのち、
PostNEMDThermalConductivityFeature
を用いることで熱伝導率を計算することができます。

計算手法#

rNEMD法では、原子の速度を交換することで人為的な温度勾配を発生させます。 PostNEMDViscosityFeature と類似の手法を用いています。

rNEMD法は以下の手順を繰り返すことで、系全体での温度を変えることなく、シミュレーション領域の中央部と下部の間で温度勾配を発生させます。

シミュレーション対象の領域ををある方向（通常はz方向）に沿ってN個のスラブに分割します。
一番下のスラブから最も温度が高い原子（運動エネルギーが最も大きい原子）を見つけ出します。
その原子と同じ元素で、なおかつ最小の運動エネルギーをもつ原子を中央のスラブから見つけ出します。
この2つの原子を交換することで、高温原子を下部から中央のスラブに移動させます。

rNEMD法を実行するには、MDの手順を変更する必要があります。
これは、 RNEMDExtension を用いることで可能です。

使用例#

from matlantis_features.atoms import MatlantisAtoms
from matlantis_features.features.md import MDFeature, ASEMDSystem
from matlantis_features.features.md.post_features.rnemd_extension import RNEMDExtension
from matlantis_features.features.md import NVTBerendsenIntegrator
from matlantis_features.features.md import PostNEMDThermalConductivityFeature

atoms_SiO2 = MatlantisAtoms.from_file("assets/thermal_conductivity/a_sio2.xyz")
system = ASEMDSystem(atoms_SiO2)
system.init_temperature(293.15)
integ = NVTBerendsenIntegrator(timestep=1.0, temperature=293.15)

# rNEMD parameters
n_slab = 20
rnemd_interval = 10
n_run=1000

md = MDFeature(integrator=integ, n_run=n_run)
rnemd_extension = RNEMDExtension(rnemd_type="thermal_conductivity", n_slab=n_slab)
nemd_result = md(system, extensions=[(rnemd_extension, rnemd_interval)])

post_feature = PostNEMDThermalConductivityFeature()
post_feature_result = post_feature(nemd_result)
print(post_feature_result.thermal_conductivity)

RNEMDExtension により、速度の交換と交換された運動エネルギーの記録を行います。
rnemd_interval で何MDステップごとに速度交換を行うかを指定することができます。

系が平衡に達するまでMDを行うと、シミュレーション領域の中央部は高温、底部は低温になります。
そして、高温領域と低温領域の間に一定の温度勾配が形成されます。

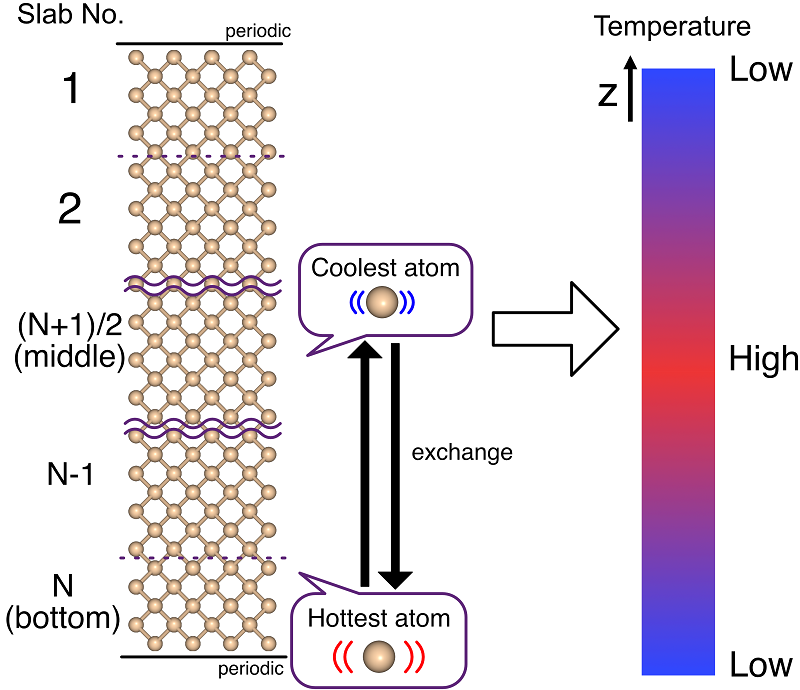
../_images/thermal_conduct_NEMD.png — Illustration of the NEMD method for thermal conductivity calculation.#

rNEMD計算を行った後、 PostNEMDThermalConductivityFeature を使うことでrNEMDのトラジェクトリを分析できます。
熱伝導率は以下のように計算されます:

[lambda = – frac{sum E_{kinetic, hot} – E_{kinetic, cold}}{2 t S_{xy} }]

(lambda) は熱伝導率、 (t) は時間、 (S_{xy}) はxy面の面積、 (frac{partial T}{partial z}) は (z) 方向に沿った温度勾配を表します。

使用上の制約#

この手法では格子による熱伝導率のみが計算されます。電気伝導による熱伝導率は考慮されていません。
金属の計算では、電気伝導による熱伝導率が重要になるので、ご注意ください。
シミュレーション領域はフォノンの平均自由行程よりも十分大きくとる必要があります。そうでないと、熱伝導率が大幅に過小評価されてしまいます。
結晶中のフォノンは非常に大きい平均自由行程をもつので、大きなシミュレーション領域が必要になります。
しかし、PFPで計算できる系のサイズの限界から、完全な結晶での熱伝導率計算は困難です。
そのため、この手法は主に液体やアモルファスでの使用が想定されています。

Tips#

スラブ数 n_slab は偶数である必要があります。
PostNEMDThermalConductivityFeature での分析を実行するには運動エネルギーの交換を記録した情報が必要なため、
RNEMDExtension を適用した MDFeature の出力トラジェクトリを使用する必要があります。
温度勾配の線形性に注意してください。もし線形性が見られない場合、MDシミュレーションの時間を長くするか、速度交換の頻度を高めてください。