PFPについて

目次

PFPは、Neural Network Potentialの一種で、密度汎関数法(DFT)の精度に迫る汎用的な原子間ポテンシャル(分子動力学ポテンシャル、force field)となることを目標として開発されました。

PFPの特長は汎用性と計算速度にあります。汎用性について、PFPは

• 可能な限り系の元素種およびその組み合わせに対して制約がかからないこと
• 分子構造や結晶構造などの静的な構造にとどまらず、化学反応や結合の組み換えを含むダイナミックな系を扱えること

を目標に設計されています。
また、計算速度について、これまで汎用的な原子シミュレーションを行う際、従来はDFTなどの計算コストが大きい手法の利用が不可欠でした。PFPは汎用性を保持しつつ、圧倒的な計算速度によって、数万原子オーダーの系や数百万ステップの動力学計算のような、DFTでは実行不可能なスケールのシミュレーションを可能にします。

この文書は3つのパートに分かれています。PFPのアーキテクチャ、データセット、およびサポートされている計算対象に関する説明です。

なお、この文書とは別に、論文[1]も公開されています。Neural Network Potentialの研究におけるPFPの位置づけや、PFP(バージョン0)を利用した応用例などが記載されています。

• アーキテクチャ解説

このパートでは、PFPで用いられている機械学習モデルの構造や内部で行われている演算の性質について解説します。アーキテクチャの細部の開示はしていませんが、保存則や不変性といった、シミュレーションを行う上で重要となるいくつかの性質を中心に記載しています。

• 学習データセット

PFPの推論性能や適用範囲はデータセットの内容に大きく依存します。このパートでは、PFPの学習に用いているデータセットの内容についての情報を提供します。

• サポートされている計算対象

このパートでは、現在のPFPの適用範囲、および適応範囲外となる系についての情報を提供します。

原子間ポテンシャルとグラフ表現について

PFPのアーキテクチャはGraph Neural Network (GNN)に分類されます。GNNはグラフで表現されるデータに対してニューラルネットワークを適用する技術の総称で、近年急速に発展している分野の一つです。

原子の振る舞いをGNNで表現することは、次の2つの意味を持ちます。1つ目は、原子系をグラフ、つまり原子およびそれらのつながりで表現しているということです。これは、十分離れた原子は互いに直接的な相互作用がないというモデルになっています。通常の古典ポテンシャルでも同様のモデル化がなされています。なお、グラフによるモデル化とはいっても、原子の位置関係に関する情報を無視するモデルになっているわけではありません。互いの位置関係(例えば距離や角度のような情報)をグラフに埋め込んで表現しています。つまり、DFTであれば電子密度として表されるような空間的な情報が、グラフのノードやエッジの情報として埋め込まれていることが期待されています。このことに関して、不変性の観点から後ほど説明します。

2つ目は、グラフに対する回帰モデルとしてGNNを使っているという点です。GNNでは、あるノードやエッジの情報がグラフを通して伝搬していくことを、graph convolutionの多段化によって明示的にモデル化しています。原子系の言葉で書き直すと、局所的な状態(ここでは電子状態のことを指していると考えてください)が、結合を伝って遠距離まで影響を及ぼしている様子をモデル化しようとしている、ということができます。このことは原子系ではごく自然な現象と考えられます。化学結合は複数の軌道が混ざり合って作られると捉えることができます。隣接した複数の結合が相互作用することはよく知られていますし、電子軌道が局所化されず広がった描像によって性質が説明される構造も数多くあります。これに関連して、相互作用の局所性の観点から以下の項目で詳しく説明します。

相互作用の局所性

PFPは、完全な局所相互作用モデルとなるように設計されています。これは、ある局所的な構造の情報が無限の距離を伝播することはない、ということを意味しています。

このアーキテクチャでは、もし十分に距離の離れた複数の分子が系に存在した場合、これらの間に相互作用がないことが保証されています。例として、十分に距離の離れた分子Aと分子Bがあった場合、分子Bがどのような状態であっても(静止していても、化学反応の最中であっても、またシミュレーション中のある瞬間に人為的に消し去ったとしても)、分子Aには原理上影響がないことが保証されます。この設計は計算コストの観点からもメリットがあります。
(余談ですが、一般的な古典的なポテンシャルには局所相互作用モデルが採用されていますが、QEq法(電荷平衡法) [2] のように密な相互作用のモデルを持つものもあります。このような場合では実際に超遠距離の原子が互いに影響することがあります。)

一方で懸念点としてあげられるのは、真に長距離間ではたらく相互作用に関する再現性です。代表的な例としては真空中のイオンがあげられます。裸のクーロン相互作用は距離に対して-1乗で影響する長距離なものとなっているためです。ただし、物質中ではこの性質は遮蔽効果によってある程度弱められることもあり、短距離の相互作用としてよくモデル化できることが知られています。

PFPは相互作用距離に関連する2つの値を持っています。まず、原子が直接的に相互作用をする距離(グラフとしてエッジがはられている状態に相当)で、カットオフ距離と呼ばれるものです。
PFPはカットオフ距離が原子ごとに可変となるアーキテクチャとなっています。原子の周囲に他の原子が存在しないときはカットオフ距離が伸び、最大で9 Å (1 Å = 10^-10 m)となります。この効果により、表面や真空中の分子といった疎な環境において長距離の直接相互作用を表現することが可能となります。反対に原子の近傍に多数の原子があるときにはカットオフ距離が短くなります。これは、長距離相互作用が近距離原子の存在により遮蔽されていることをモデル化しています。この場合の相互作用は主にグラフ畳み込みの積層による近距離相互作用を介しての間接的な遠距離相互作用として表現されます。
なお、PFP v5.0.0以前はカットオフ距離は6 Åで固定です。

次に、ネットワークを介した相互作用の距離が考えられます。原子のネットワークは上記のカットオフ距離で決まりますが、GNNのレイヤーが多段になっているため、原子の情報はネットワークを介して隣の隣へと伝播していきます。これによってある原子がアーキテクチャ全体を通して相互作用する距離はカットオフ距離の何倍も長くなりえます。物理的には、金属結合やπボンドを介した相互作用など、いわゆる電子軌道がつながっていることにより発生する長距離相互作用がこれに対応した現象であると考えられます。PFPでは、この値(結合を介した影響範囲の距離)が最大で20 Å 以上になるように設計しています。

つまり、GNNによって、相互作用は局所的であるとするモデルを維持しつつ、結合を介した相互作用に関してはより長い範囲(ここでは20 Å)まで考慮できるようになっている、と考えることができます。

GNNで使われる情報と不変性

GNNでどのような情報を使うかはアーキテクチャ設計の一翼を担っており、研究対象となっています。この章では、不変性との関係を軸に概要を紹介した後に、PFPではどのように扱っているかの説明を行います。

原子の構造として入力される情報は、系のすべての原子の種類と3次元座標です。基本的にはこれがGNNに使える情報のすべてです。ただし、この情報をそのままの形で使うのは問題があります。たとえば、顕著な問題として、座標変換のような本質的でない変換に対して入力される値が変わってしまうということです。不変性を保つことが保証できなくなってしまうため、様々な問題を引き起こします。

この問題に対処するため、一般には様々な物理的な対称性に対して出力(ここではエネルギー)が不変となることが要請されます。これは学習によって担保する方法と、アーキテクチャの設計時に明示的に不変性を保つようにする方法の2種類の解決策があります。

PFPは後者の立場をとっています。不変性を高いレベルで保つことによって、分子動力学シミュレーションとしての使いやすさと汎化性能の両方に良い効果をもたらすと考えているためです。

一方で、入力される情報を制限しすぎると、アーキテクチャの表現力を抑制することにもつながってしまいます。例えば、入力される情報を座標変換に対して不変なものとするため、グラフの結合距離の情報に絞って使うことが考えられます。[3] これは広く受け入れられている手法ですが、入力を距離情報のみに制限してしまうと結合角度の情報が明示的に与えられなくなります。そこで、結合距離に結合角度などの情報を組み合わせて使用する方法が使われています。

また、出力が不変であればよく、入力には必ずしも不変量を使う必要はないため、座標変換に対して共変な幾何的量を入れるなどの試みも近年では研究が進められています。 [4]

このように、なるべく入力情報を取りこぼさず、特に電子状態に影響する量を明示的に扱いつつ、不変性を保持することがアーキテクチャ設計における要点となっています。

PFPでも位置関係に関する高次特徴を使用していますが、以下の不変性が保たれるようにアーキテクチャを設計しています。

• 並進不変性
• 回転不変性
• 鏡像反転不変性

これにより、動力学計算中に不自然な外力がかかるようなことがないようにしています。

また、近距離相互作用モデルであることから、空間的に隔たれた2つの分子についてはそれぞれ独立に並進不変性や回転不変性が保たれます。さらに、エネルギーが示量性である(系がある部分系の和でつくられるとき、エネルギーも部分系の和になる)ことも保たれています。

上記の幾何的な不変性とは別の話として、系にある原子の集合は通常リストとして表現されますが、この順序を交換しただけのものは物理的に等価のため、順序の交換に対してエネルギーは変化しません(順序の不変性)。これはGNNが入力をグラフとして表現することにより自然に保証されます。

またこれとは別に物理的な要請から時間の並進不変性と時間反転不変性も必要ですが、これらはポテンシャルとは別に一般的な分子動力学法の各種手法を通して保証されるものです。

エネルギー

エネルギー曲面の滑らかさ

MDのように長時間の動力学計算を行う際、エネルギー曲面の滑らかさはシミュレーションの安定性に直結する問題です。また、直接シミュレーションに必要な力はエネルギーの1階微分に対応する量ですが、例えば弾性率のように、物理量によってはより高階の微分値に相当する量が必要になることがしばしばあります。このことから、PFPではエネルギー曲面の滑らかさは学習によってではなくアーキテクチャとして常に保存されるよう設計されています。

具体的には、原子の位置に対してエネルギーが高階まで微分可能であるように設計されています。これには以下の性質が含まれています。

• 任意の原子のペアについて、カットオフ距離をまたいだ際にエネルギーが不連続に変化しない
• 同様に、カットオフ距離をまたいだ前後で力が不連続に変化しない
• 任意の入力に対して、2階以上の高階微分が存在

最後の性質は、BFGS法のようなHessianの存在を仮定する手法を適用する際にも重要な性質となります。

ただし、上の記述はアーキテクチャの数式上での話であり、これとは別に、コンピュータにおける数値の精度が有限であることによる計算誤差が発生することに注意してください。

エネルギーの基準点

エネルギーの基準点は、真空中の単原子を0ととるように設定しています。現在ではこれは学習によって担保するようにしています。つまり、真空中の無限遠点は厳密にはちょうど0からずれることがあります。これはエネルギーの微分値を使う動力学計算や複数の構造間のエネルギー差を議論する際には問題にはなりませんが、真空中の無限遠点とのエネルギー差を厳密に議論したい場合には(DFTと同様に)ゼロ点エネルギーが存在することになるため気をつけてください。

近距離反発

一般に、系の中のある2原子を平衡距離より近づけていくと、核反発の効果によりエネルギーが大幅に上昇していきます。これはPFPでも再現することができます。ただし、多数の原子を現実的でない原子間距離に同時に置いた場合に、DFTとコンシステントなエネルギーを必ずしも再現せず、場合によっては低いエネルギーを出力することがあります。現在のPFPではこのような入力に対して特別に警告やエラーを出すことはないため、原子の初期配置には注意が必要です。

エネルギー以外の物性値

力はエネルギーに対する原子の位置の微分で定義されます。PFPでも力はエネルギーを微分することによって計算されています。エネルギー曲面は滑らかになるようにしているため、計算された力とエネルギーは(数値計算誤差を除いて)互いにコンシステントです。

また、応力はビリアルの式によって計算されます。これも同様にエネルギーのセルサイズに対する微分で計算されます。そのため応力とエネルギーも互いにコンシステントです。

内部的には、力と応力はNNのback propagationを使って計算されています。また、実装上は力と応力は一度の微分で同時に計算されます。

例外的な出力がchargeです。これはエネルギーの推論時に副次的に推論した量であり、現在は実験的な出力と位置づけています。現在は下記の結晶系学習データから求められたBader chargeを推論しています。chargeに関しては系全体の合計値が0になる拘束条件を与えています。
電子密度分布は本来空間分布するものなので、エネルギーや力と違い、原子に対するchargeという量を定める際には追加の定義が必要です。Bader charge解析は広く用いられている手法ではありますが、妥当な値が得られない場合があり、実際に学習データにも妥当でない値があることが確認されています。
これらの定義や手法に起因するばらつきに加え、chargeを副次的な値と位置づけていることから、学習時にエネルギーや力と比較して、厳密に合わせることを重視していません。このため、chargeの再現性はエネルギーや力の再現性と比較して、低くなっています。
chargeに関するこれらの方針を変更することは検討しておらず、再現性が大きく改善することもないと考えています。

単位系

PFPでは、出力されるエネルギーの単位はeV、また入力される構造の長さの単位はÅとなっています。力や応力の単位はこれらの複合単位で、力についてはeV/Å、応力についてはeV/Ųです。chargeの単位は電荷素量です。

周期境界

PFPのアーキテクチャでは、周期境界に対しても特別な処方をすることなく、同一のアーキテクチャで表現することができます。これは、相互作用の局所性、および並進不変性が保たれていることによるものです。

また、周期境界の系についてある軸に対して2周繰り返した系は、原子の位置を動かさなければもとの系と等価な系であることが期待されます。具体的には、系全体のエネルギーはもとの系のちょうど2倍となり、すべての原子にかかっている力はもとの系と同じであることが期待されます。これもエネルギーの示量性によって担保されています。

なお、周期境界でない自由境界の場合には、物理的には無限に真空が広がった系をシミュレーションしているものと考えられます。このときは応力は出力されません。

DFT計算を行い独自のデータセットを構築し、PFPの学習に用いています。

構造

PFPの学習データには、分子系のデータと結晶系のデータが存在します。

汎用的なポテンシャルを開発するためには、多様な構造を学習させる必要があります。また、最安定構造だけでなく、不安定な構造や現実には存在しない様な構造も学習させることが重要です。
様々な分子や結晶構造の安定状態や変形させた構造を生成・計算することで、安定状態のみならず、高温でのMDや、遷移状態、吸着状態と言った多様な状態を再現できるよう努めています。

計算条件

PFPには、分子系、結晶系(Hubbard補正なし)、結晶系(Hubbard補正あり)の3つのモードがあります。各モードでは、それぞれの学習データの計算条件でのエネルギー・力を推論します。いずれのモードにおいても、系全体の電荷は0としています。

分子系

分子系では、ωB97xd汎関数、6-31G(d)基底を用いたDFT計算によりデータを構築しています。O₂などの2原子分子を除き、スピンはsingletあるいはdoubletとしており、triplet以降は考慮していません。H2の解離などの波動関数の対称性が崩れる系を考慮し、非制限DFT (Unrestricted DFT) を用い、軌道の対称性を崩した計算を行っています。なお、分子系ではH, C, N, O, F, P, S, Cl, Brの9元素のみがデータセットに含まれています。

結晶系(Hubbard補正なし)

結晶系では、PBE汎関数とPAW型擬ポテンシャルを用いています。分散力補正は行っていません。

カットオフ・k点サンプリング

カットオフエネルギーは、全ての系において520 eVとしています。k点サンプリングは 1000 k-point / reciprocal atomとしており、a, b, c軸の長さの逆数に比例させています。ただし、真空中に分子を置いた系などでは、Γ点のみとしています。なお、真空層の大きさは10Åを基本としていますが、6Åで計算したものも含まれます。

Smearing

様々な系に対して同じ条件で計算するため、Guassian smearingを用い、smearing幅は0.05 eVとしています。

スピン・磁性

スピン分極は考慮していますが、スピン軌道相互作用やnon-collinear磁性は考慮していません。より安定なスピン・磁性での結果を採用しています。例えば、反強磁性・強磁性の2つが考えられ、反強磁性の方がエネルギーが低い場合、反強磁性を採用しており、PFPでは反強磁性での値のみを推論することが出来ます。ただし、考えられる全てのスピン・磁性での計算を行うことは困難であることから、計算対象に応じて、強磁性のみでの計算を行っているケースも存在します。

収束判定

SCFの収束判定(EDIFF)は10^-4 eVとしており、収束しなかった計算は全て除外しています。

Charge

BADER chargeを計算しており、この値をchargeとしています。

擬ポテンシャル

VASP5.4.4、及び、VASP6.4.0に付属しているPBE向けのPAWポテンシャルを擬ポテンシャルとして用いています。
これら2つのバージョンに付属するPAWポテンシャルは同一であることを確認しています。
各元素の擬ポテンシャルの選択は、以下の図に示す通りです。

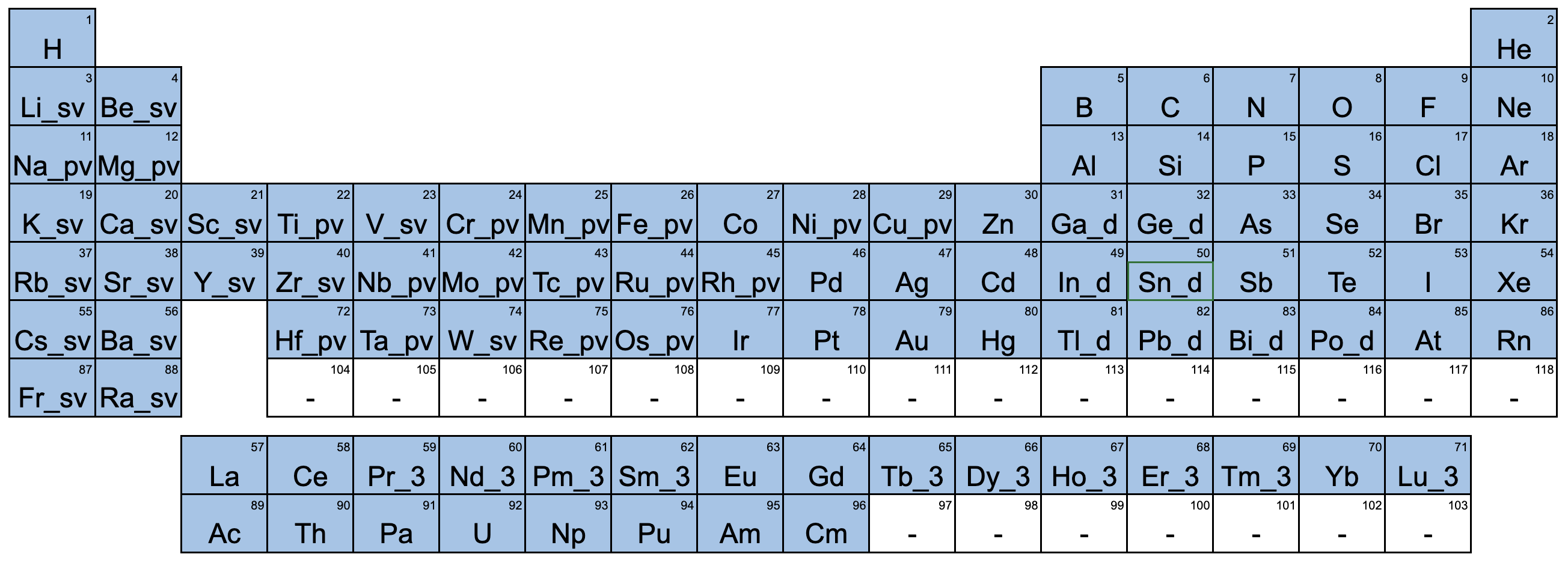
なお、擬ポテンシャルの非局在項を求める際の射影演算子の評価は、波数空間ではなく実空間で行わせています。

VASP Version

PFP v4.0.0以前は、結晶系に関する全てのデータを、VASP5.4.4を用いて構築していました。
PFP v5.0.0以降では、DFT計算の高速化を目的として、VASP6.4.0を用いて構築したデータが含まれています。
比較検討の結果、VASP5.4.4とVASP6.4.0とでは、SCF計算の収束に起因する誤差の範囲内で、全エネルギーを含めて同一の結果を返すと判断しています。
なお、これはあくまで社内の判断であって、VASP5.4.4とVASP6.4.0が同一の結果を返すことを保証するものではないことに注意して下さい。

VASP6.4.0による計算では、SYMPRECの値をVASPのデフォルトである10^-5から10^-8に変更しています。
これはVASPの実行時に発生する対称性に関するエラーを回避するためのものです。
これ以外の計算条件は、VASP5.4.0と同一のものを利用しています。

結晶系(Hubbard補正あり)

結晶系(Hubbard補正あり)では、PBE汎関数とPAW型擬ポテンシャルを用いています。分散力補正は行っていません。
Hubbrard補正(GGA+U計算)を行っていることを除き、結晶系(Hubbard補正なし)と同一の計算条件です。

GGA+U

結晶系(Hubbard補正あり)では、全ての系においてGGA+U計算を行っています。Fe単体等に対しても適用しているため、注意が必要です。例えば、FeのBCC格子など一部の構造に実験値との差異があります。Dudarev[5]らによって提案された手法での、U-Jは以下の値を用いています。

	V	Cr	Mn	Fe	Co	Ni	Cu	Mo	W
U-J (eV)	3.25	3.7	3.9	5.3	3.32	6.2	4.0	4.38	6.2

元素の対応状況

現在のPFP (v7.0.0以降) は、HからCmまでの全ての元素を再現する対象として注力しています。

なお、現在のPFP (v7.0.0以降) では対応状況がExperimentalに相当する元素は無くなりました。PFP v6.0.0まででExperimentalとしていた元素は「十分な量の訓練データが存在しない、または、検証による満たすべき再現性を確認できていない元素」であり、「部分的に再現できる可能性がある一方で、今後のバージョンで再現できなくなる可能性がある元素」でしたが、現在のPFPではその様な元素はありません。

• Expected: 現時点でPFPが再現する対象として主に注力している元素。
  • HからCmまでの全ての元素（擬ポテンシャルの周期表にて、青色で色付け）。
• Unexpected: 再現できないもの。
  • Bk以降の全ての元素。

計算モード

先述のように、PFPは3種類のDFT計算条件による学習データを持っています。これに対応して、計算モードと呼ばれる機能を提供しています。計算モードを切り替えることによってどちらの学習データに合った挙動をするかを選べます。PFP v4.0.0以降におけるデフォルトは結晶系(Hubbard補正なし):CRYSTAL_U0です。これ以外に結晶系(Hubbard補正あり):CRYSTAL、および、分子系:MOLECULEがあります。PFP v3.0.0以前におけるデフォルトはCRYSTALであり、PFP v4.0.0以降とは異なることに注意してください。

CRYSTAL_U0を最も基本的なモードと位置づけています。酸化物など、Hubbard補正が有効な系に対してはCRYSTALを利用すると再現性が向上します。MOLECULEは単分子を主眼としたモードです。分子の安定構造や反応の遷移状態を求める場合等には適していますが、液体等の分子間の相互作用が重要となる系の再現性は低いと考えられます。

計算される物理量の種類はいずれも同じです。分子系モードに切り替えた場合でもデータセットの9元素以外の計算も実行可能で、chargeも出力されますが、これは結晶系データから外挿された値となっています。

現行のPFPのスコープ外とされる対象

以下の系・現象・計算条件などは、現行のPFPのスコープ外です。

• 励起状態など、電子状態として安定状態ではない状態の再現
• 系全体の電荷がニュートラルでない構造
• DFTの精度を超えたエネルギーの再現精度
• HOMO/LUMOなどの電子物性
• 粗視化した分子動力学モデル

将来的には、適用可能対象の拡大や、別の推論モデルと組み合わせた新しい計算フレームワークを作るなどの発展の可能性があります。

[1] So Takamoto, Chikashi Shinagawa, Daisuke Motoki, Kosuke Nakago, Wenwen Li, Iori Kurata, Taku Watanabe, Yoshihiro Yayama, Hiroki Iriguchi, Yusuke Asano, Tasuku Onodera, Takafumi Ishii, Takao Kudo, Hideki Ono, Ryohto Sawada, Ryuichiro Ishitani, Marc Ong, Taiki Yamaguchi, Toshiki Kataoka, Akihide Hayashi, Nontawat Charoenphakdee, and Takeshi Ibuka, “Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements,” Nature Communications 13, 2991 (2022). https://doi.org/10.1038/s41467-022-30687-9

[2] A. K. Rappe and W. A. Goddard III, J. Phys. Chem., 95, 3358-3363 (1991).

[3] K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko, K.-R. Müller, 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA (2017).

[4] Brandon Anderson, Truong-Son Hy, Risi Kondor, 33rd Conference on Neural Information Processing Systems, Vancouver, Canada (2019).

[5] S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 57, 1505-1509 (1998).

2024.09

以下の項目をPFP v7に対応させました。

• 「擬ポテンシャル」の図を更新しました。新しくサポート対象となった元素が増えました。
• 「元素の対応状況」を更新しました。扱える元素の種類が72元素から96元素まで増えました。

© Copyright 2021, Preferred Networks, Inc. and ENEOS Corporation