2023.9.11
製品・サービス
PFP v4 バリデーション
概要
2021年7月のMatlantisのリリース以降、コア技術となるNNP (Neural Network Potential)であるPFP (Preferred Potential) は約半年に1回のアップデートを行い、2023年8月現在では最新版となるv4が提供されています。
ここでは、最新版となるv4の検証結果について、v3と比較しつつ紹介いたします。
計算手法
比較対象とする密度汎関数法(Density Functional Theory, DFT)計算は、VASP 5.4.4を用いて行いました。PFPの教師データ生成に用いている計算条件と同じ計算条件を用いており、PBE汎関数とPAW(Projector Augmented Wave)法を利用して計算しています。詳細についてはPFPの論文[1]を参照してください。なお、PFP v2からHubbard補正を行わない計算モードを提供しており、本検証はこれを対象としています。このため、比較対象とするDFT計算においても、Hubbard補正を行っていません。
結果
v4での改善点の一つとして、体積や密度の再現性向上が挙げられます。
ここでは、26種類の有機分子の液体の密度の再現性を実験値と比較し、検証しました。各有機分子に対して 300 K、 1気圧のNPTアンサンブルの分子動力学(MD)計算を、Grimmeらによって開発されたD3補正[2, 3]を加えたモードのPFPを利用して行い、平均密度を計算しています。
v4では、v3と比較してMAE (mean absolute error)が半分程度になっており、大きく改善しました。有機分子の液体密度は基本的な物性の一つであり、これが改善したことは大きな意義があると考えています。
有機分子の液体密度は、分子内の相互作用など比較してかなり小さい分子間の相互作用に依存しています。古典的なMDポテンシャルでは分子内と分子間の相互作用を別の項として扱いますが、PFPを始めとしたNNPでは同一に扱います。このため、様々な状態を再現する必要のある汎用的なNNPで、液体密度を再現することは困難であることだと考えていますが、様々な工夫により改善することができました。
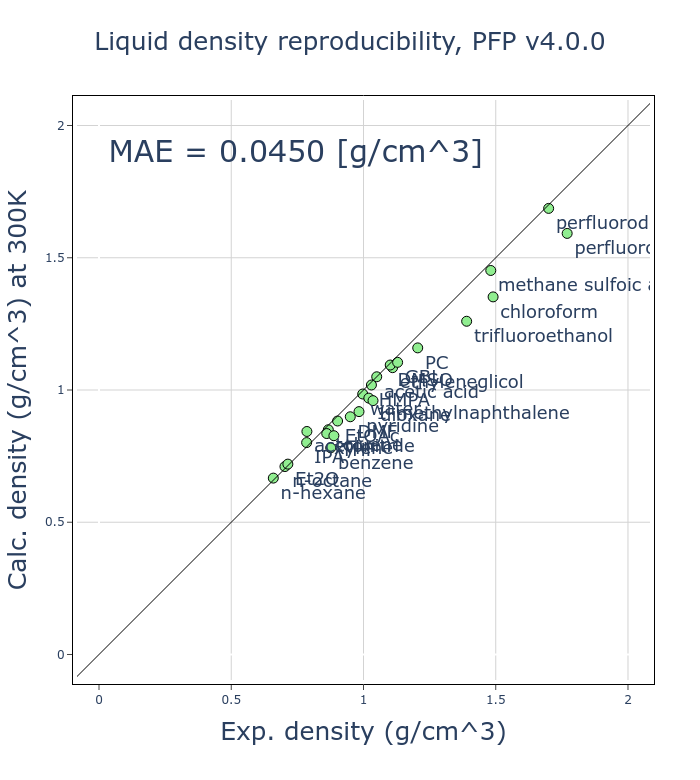
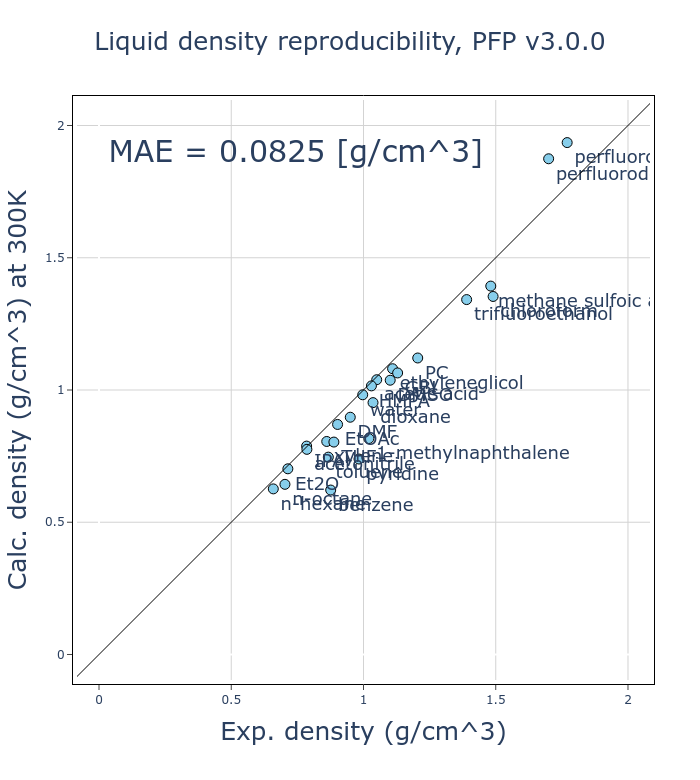
v4では、相図の再現性も向上しています。なお、ここでは温度、圧力ともに0で、組成比を変えた場合の相図を扱います。相図の再現性を検証するため、相図における凸包(convex hull)とのエネルギー差(energy above hull, Ehull)を比較しました。Materials Project [4]に登録されている1、2、3元系の結晶構造を対象とし、PFPがサポートする72元素のみに絞っています。これらの結晶構造をDFT計算とPFPとでそれぞれ格子定数を含めた構造最適化を行っています。なお、これらの結晶構造の多くはPFPの学習用データセットにも含まれています。
得られた結果をy-yプロットで示します。なお、このy-yプロットでは、DFT計算での凸包上に存在する構造は除外しています。軸とカラースケールの両方がlogスケールであることに注意してください。v4, v3のいずれにおいても、ほとんどがy-yプロットの対角線上にあり、Ehullが大きい構造から小さい構造まで、破綻なくDFT計算での結果を再現できていることがわかります。また、プロットそのものからは少しわかりにくいかもしれませんが、v4はv3からMAEで20%程度改善しています。
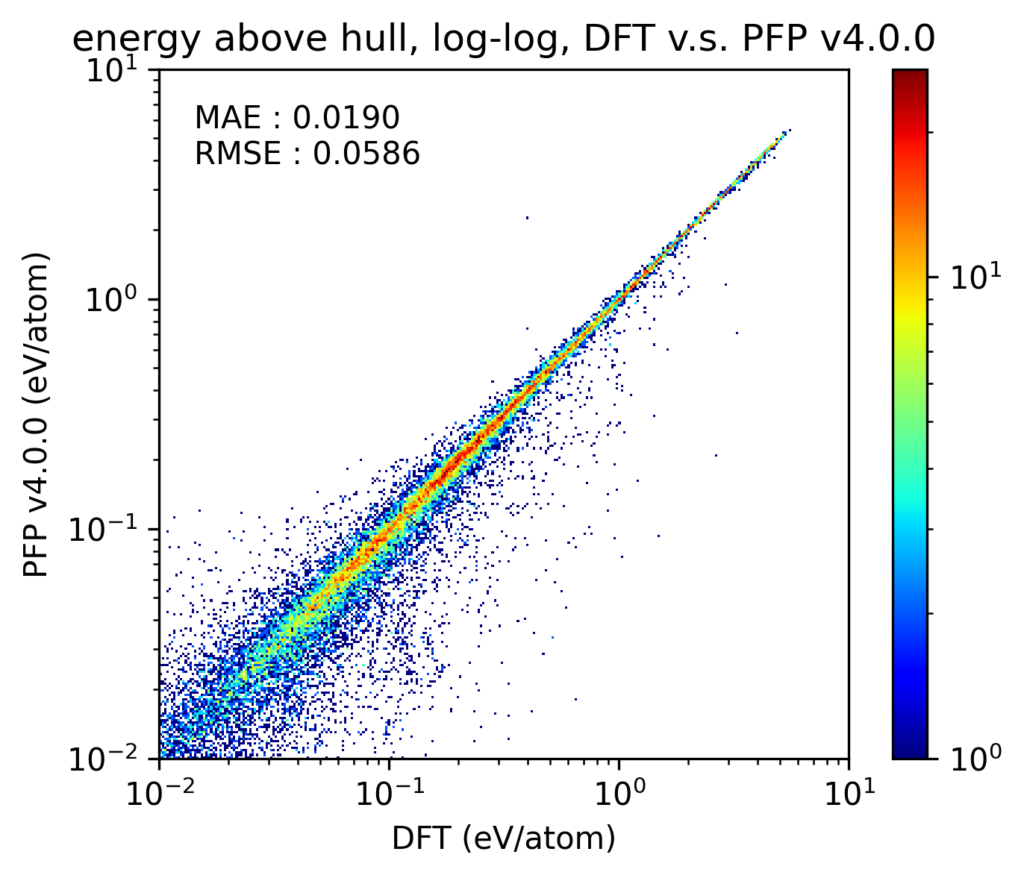
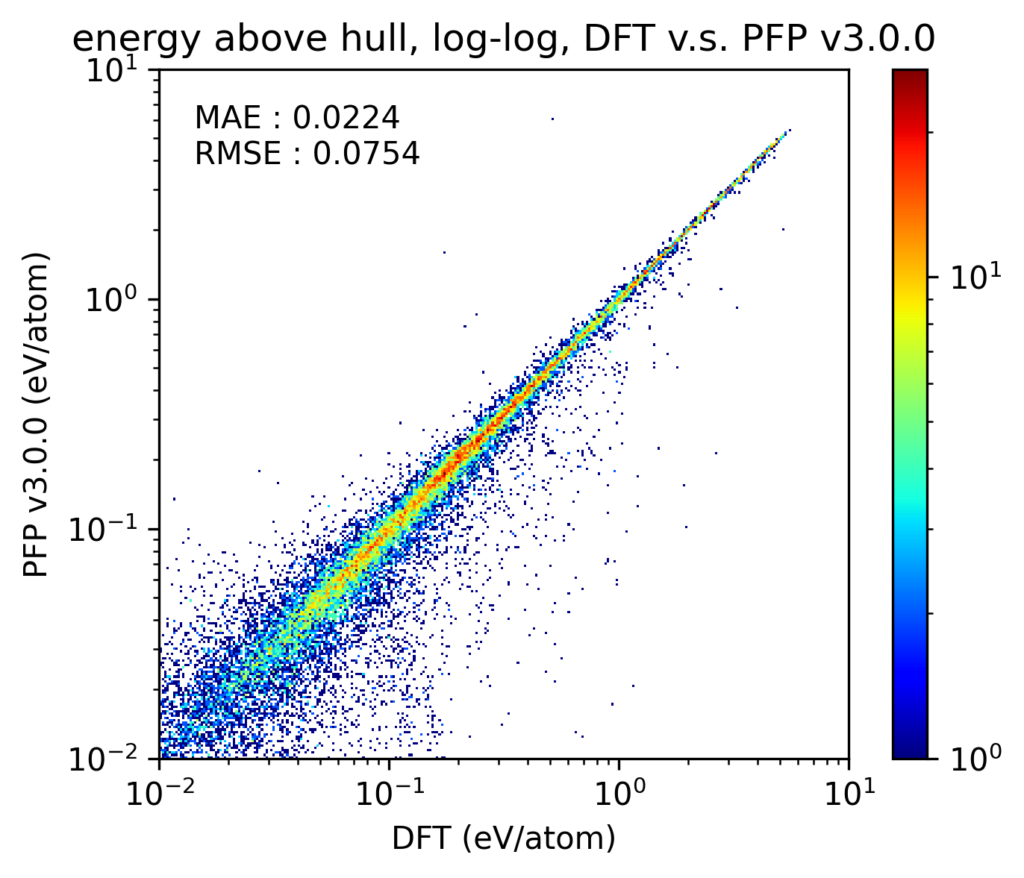
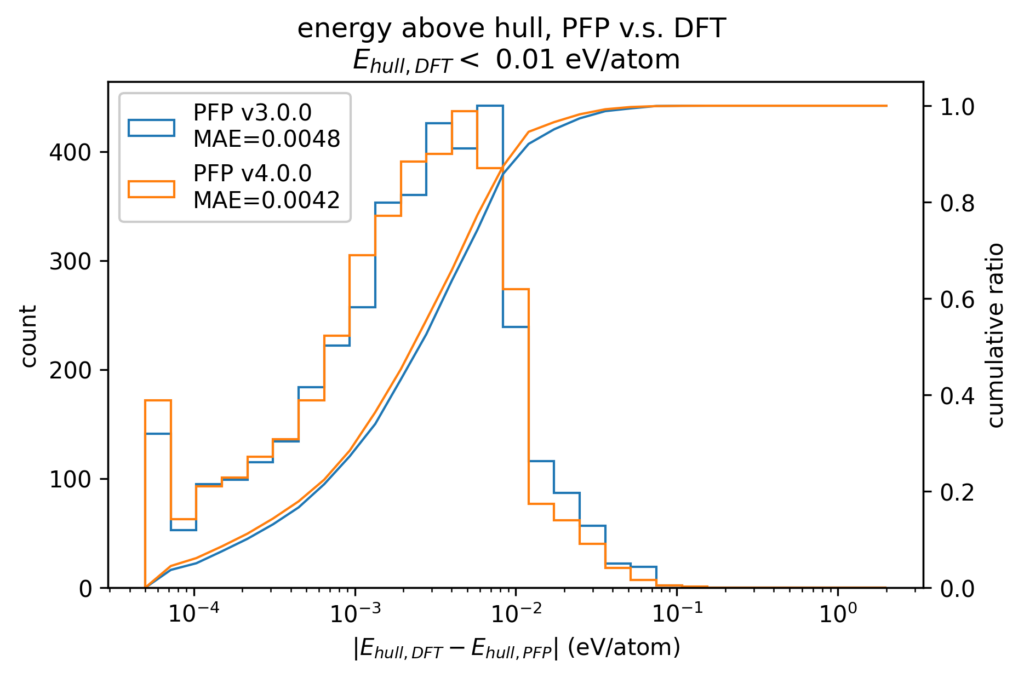
材料探索において結晶構造の安定性を評価する場合、凸包付近の構造、すなわち、Ehullが小さい結晶構造は、より小さい誤差でEhullを計算できることが求められます。以下の図は、DFT計算でのEhullが0.01 eV/atom未満の構造に絞って、DFT計算とPFPでのEhullの誤差の絶対値をヒストグラムで示したものです。DFT計算で結晶構造を探索する場合、DFT計算と現実世界との誤差を考慮し、Ehullが0.005 eV/atom程度までの構造を安定とみなすことがしばしば行われます。v4でのMAEは、v3から20%程度改善した0.0042 eV/atomとこれを下回っています。
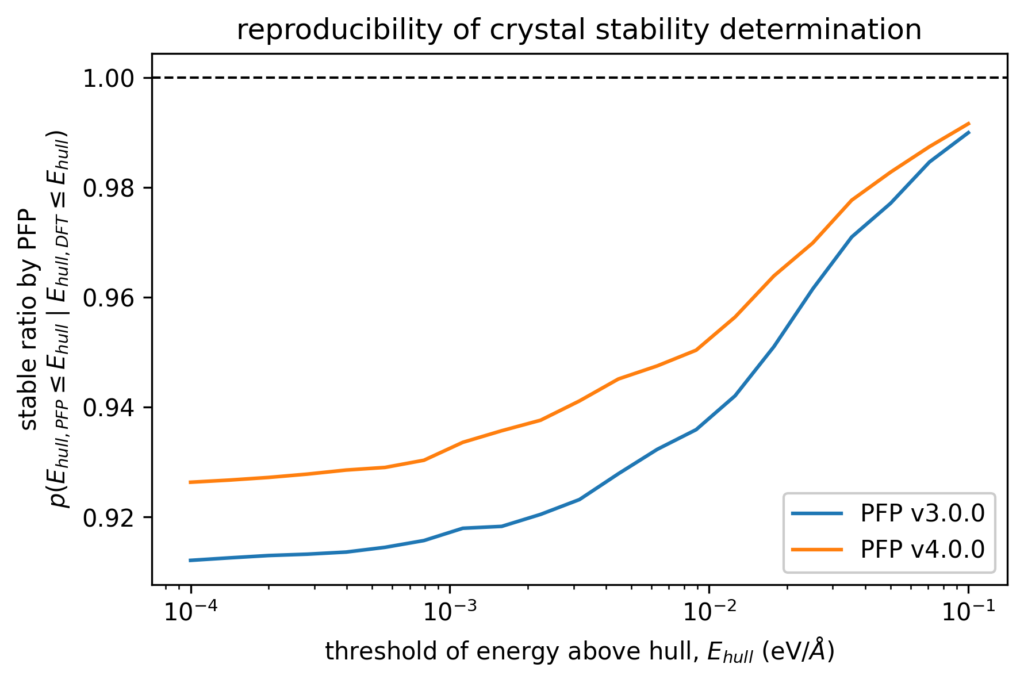
結晶構造の安定性を判定する場合を想定し、DFT計算で安定であると判定された結晶構造がPFPでも安定と判断されるかを検証しました。より具体的には、安定と判定するためのEhullの閾値を定めた際に、DFT計算でのEhullがその閾値以下となる結晶構造に対して、PFPでのEhullもその閾値以下となる結晶構造の割合を計算しています。
DFT計算での結晶構造探索でしばしば用いられる閾値である0.005 eV/atomの場合、v3では0.930であったのが、v4では0.946に向上しています。 言い換えれば、DFT計算では安定と判定される構造をPFPでは不安定と判定してしまうケースが、v3.0.0では7.0%程度存在していたのに対して、v4.0.0ではその約3/4の5.4%程度に減っています。
これらの改善によりPFP v4は、結晶構造探索に用いることができる水準に到達したと考えています。
まとめ
PFP v4の検証結果を示しました。v4では、v3と比較して有機分子の液体密度の再現性が大きく向上しました。また、相図の再現性も向上しており、結晶構造探索に用いることができる水準であると考えています。
詳細
液体密度や相図の再現性向上は、様々な構造に対するPFPのエネルギーや力、密度の再現性の向上に寄与していると考えています。以下は、Crystal Open Database (COD) [5] に含まれる結晶構造に対する検証結果です。PFPがサポートする72元素で構成される構造を対象としています。これはPFPの学習用データセットに含まれていません。ただし、学習用データセットに含まれている、Materials Projectから取得した構造に同じ構造が含まれている可能性があります。
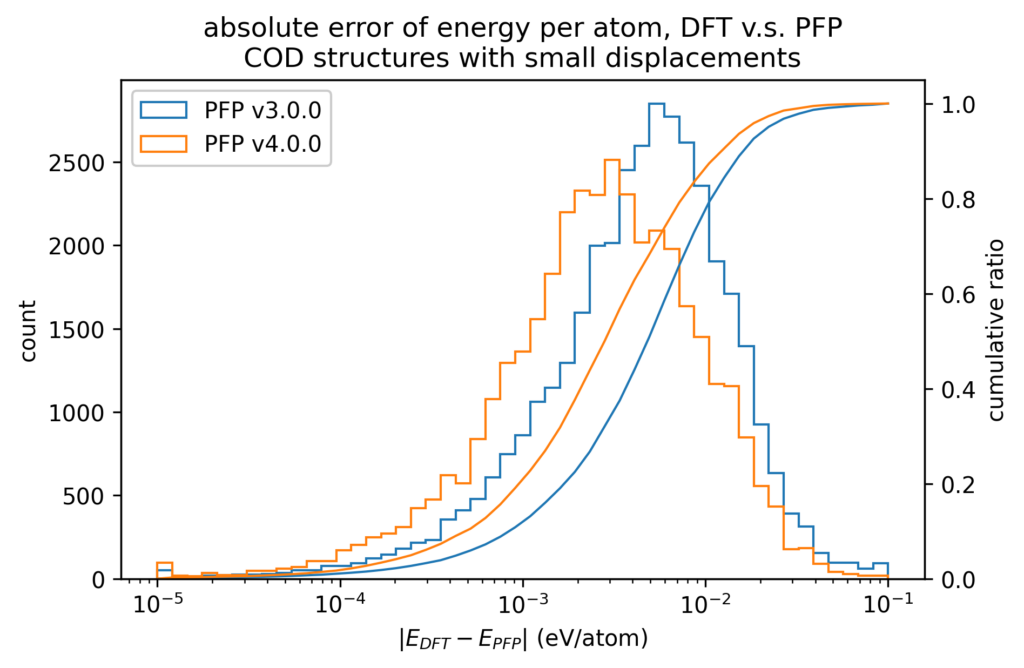
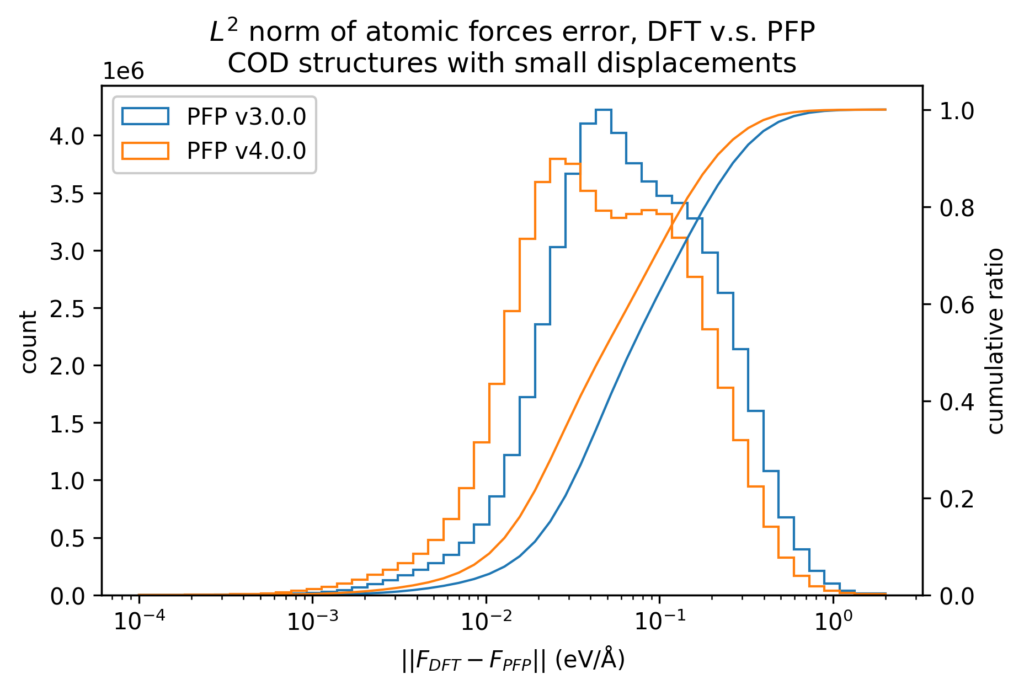
これらの結晶構造をDFT計算で構造最適化した後、原子位置に微小変位を加えた構造のエネルギーと力をプロットしました。エネルギーは原子数で割っており、真空中の単原子のエネルギーを0としています。力は各原子に働く力のXYZ成分をそれぞれ独立に比較しています。カラースケールがlogスケールになっており、赤い点一つは、青い点一つの103倍あるいは107倍となっていることに注意してください。
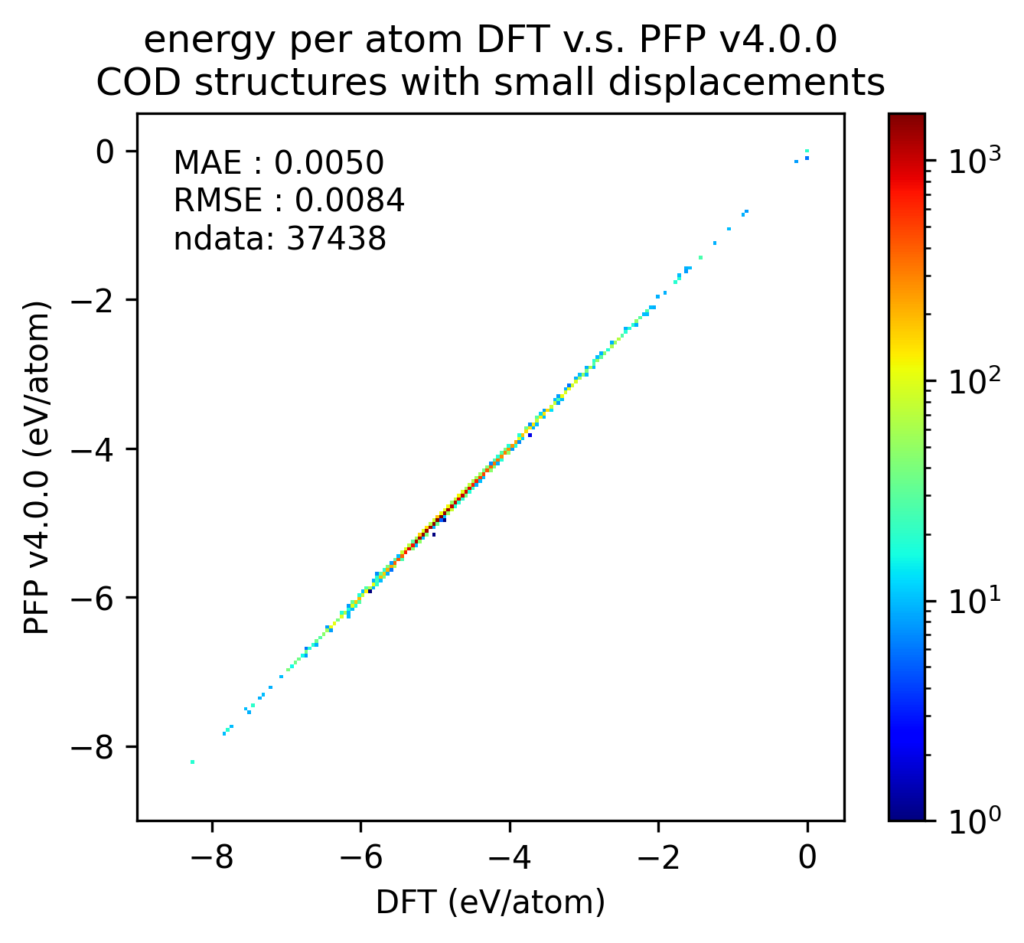
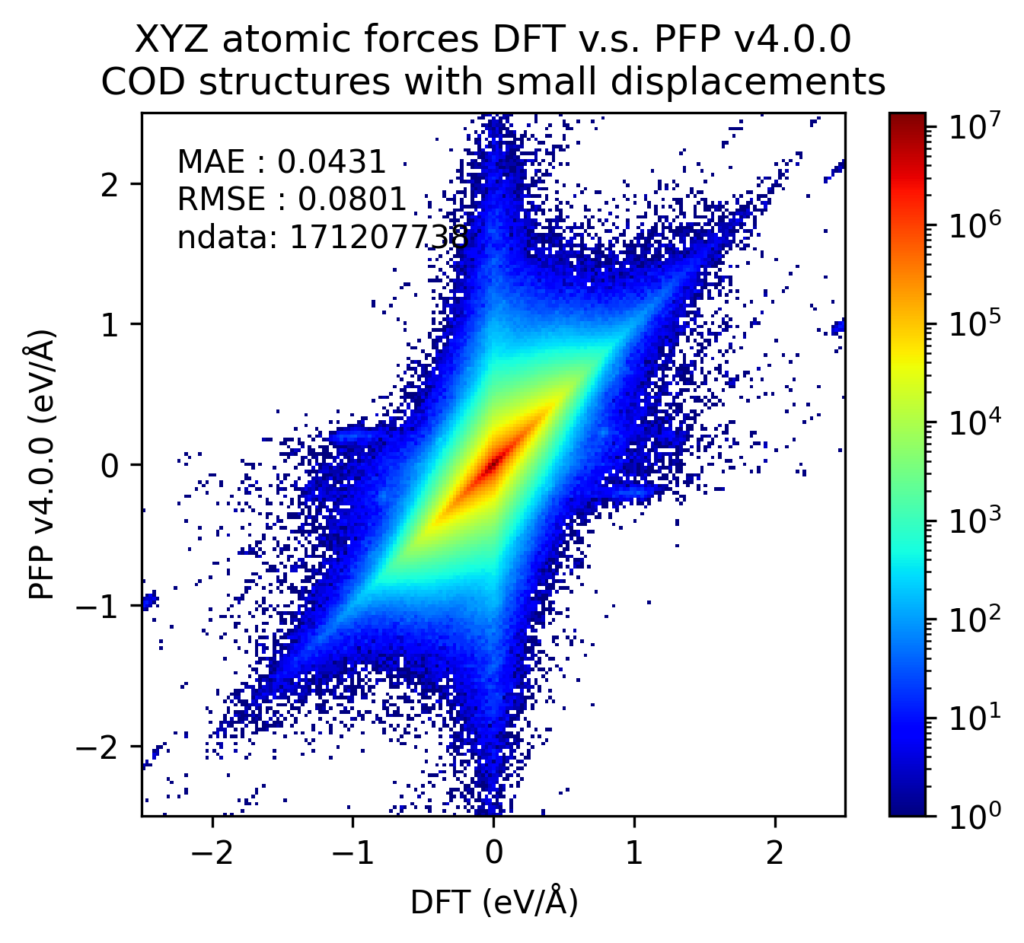
DFT計算での値とPFPでの値との誤差をヒストグラムで示します。力はXYZ成分を独立に評価するのではなく、ベクトルの差のL2ノルム(長さ)をとっています。いずれも、v4ではv3から改善しています。
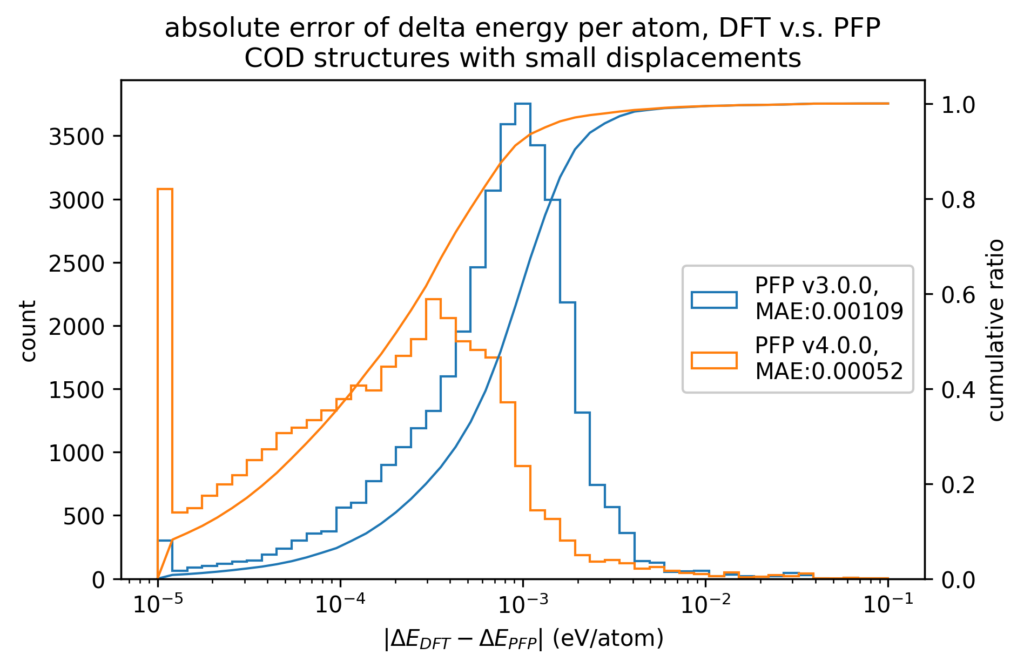
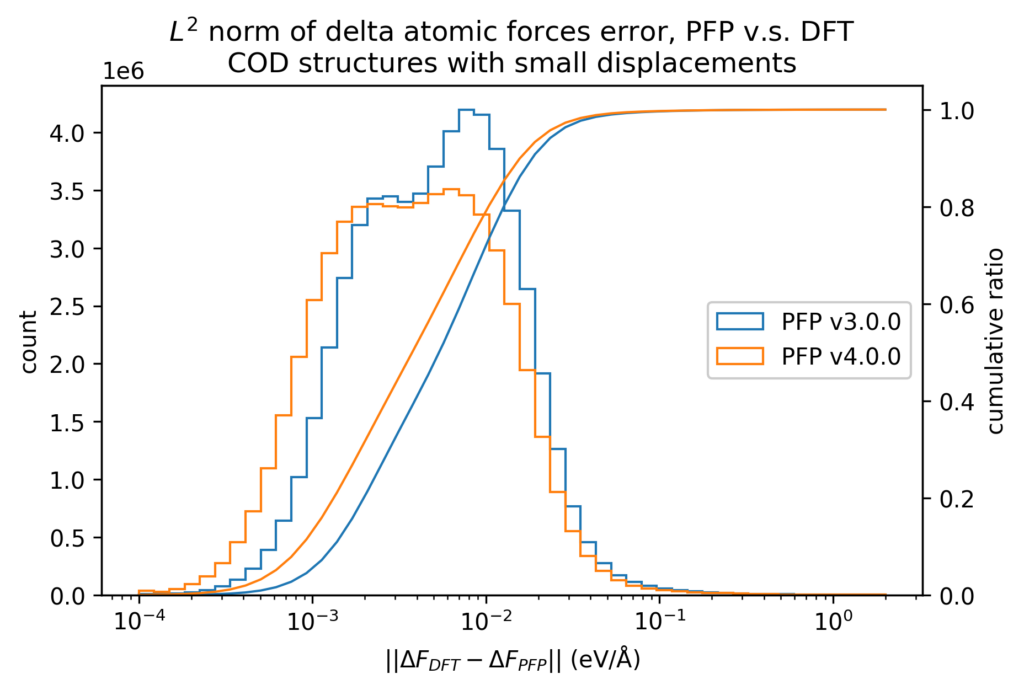
また、原子位置に微小変位を加える前後でのエネルギーと力の変化を、DFT計算とPFPとで比較しています。微小変位によるエネルギーと力の変化の誤差は、エネルギーと力に対する誤差そのものより1桁以上小さくなります。したがって、Force Constant 等の局所的なエネルギー曲面が重要となる物性値はより精度よく計算できることが期待できます。
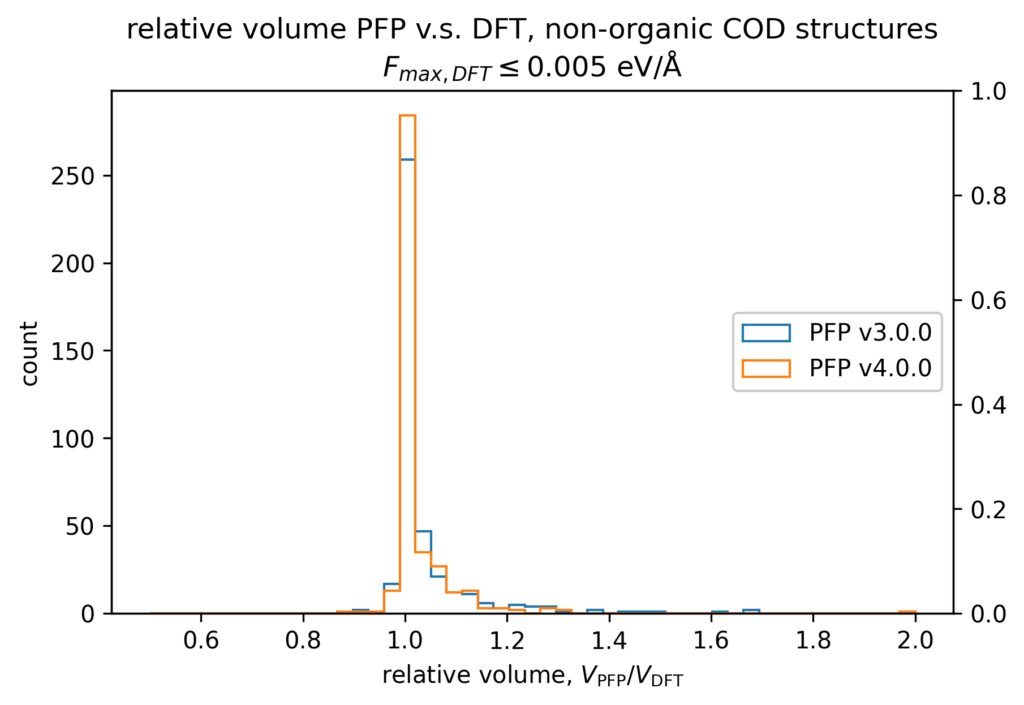
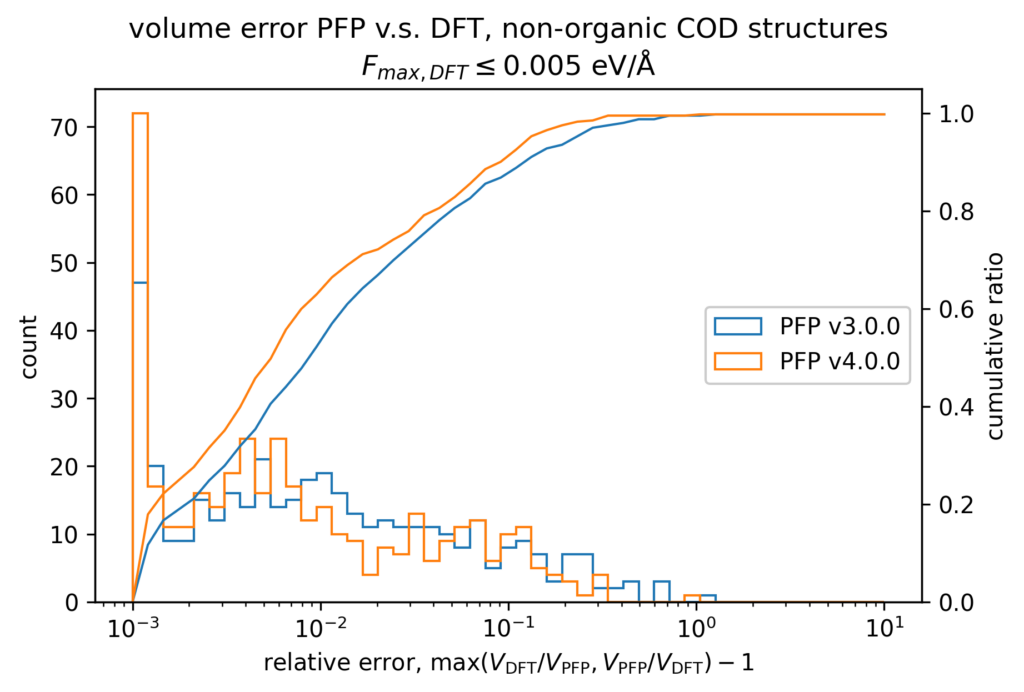
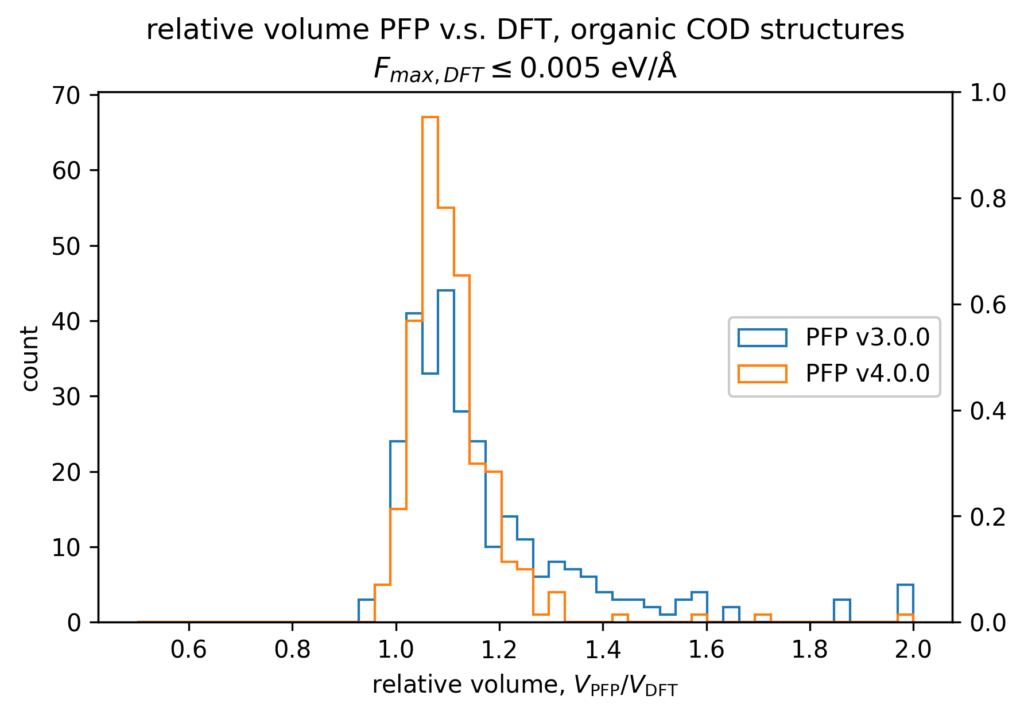
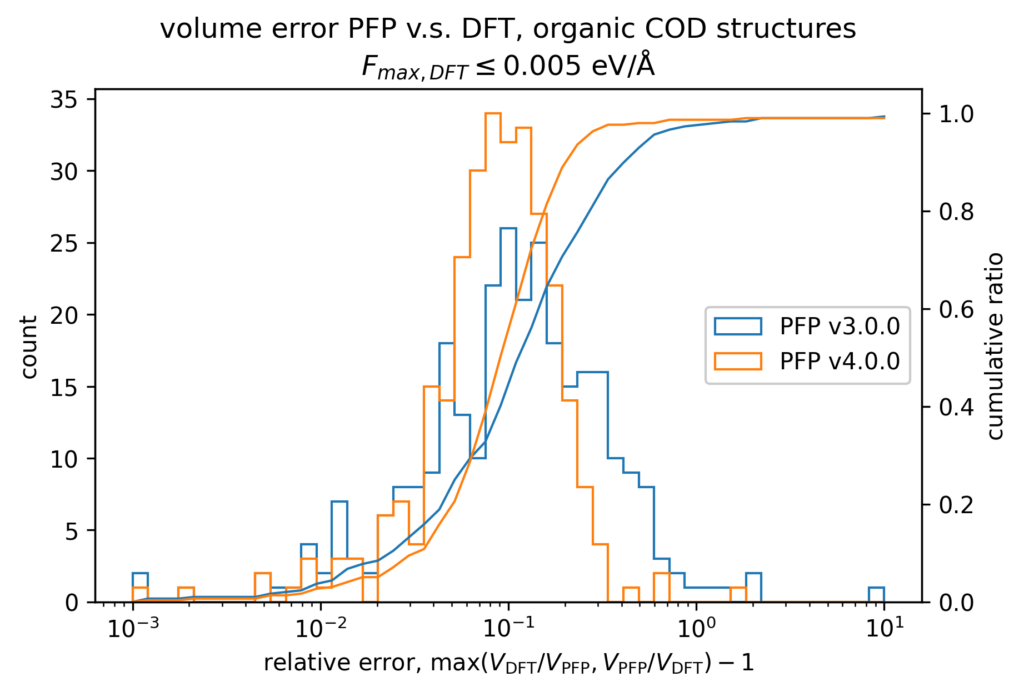
体積の再現性を以下に示します。DFT計算とPFPでそれぞれ、forceが0.005 eV/Å以下になるように構造最適化を行いました。H, C, N, O, P, S, F, Cl, Br, I のみで構成される構造をorganic、それ以外をnon-organicと分類して、別々に比較しています。v4では特に体積を大きく外す構造が減っていることが分かります。non-organicな構造の体積に関しては良い再現性を示している一方で、organicな構造の体積の再現性にはさらなる改善の余地があると考えています。有機結晶は弾性率が大きく、分子間相互作用という弱い力が関わっているため、無機結晶と比べて体積を厳密に再現することが難しいと考えています。
また、organicな構造に対しては5%程度体積を過剰評価する傾向があるため、改善すべき課題と捉えています。
Acknowledgement
PFPの最新版(v4)は、PFNのスーパーコンピュータおよび国立研究開発法人産業技術総合研究所のAI橋渡しクラウド(ABCI)を用いて開発されました。
参考文献
[1] Takamoto, So, et al. “Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements.” Nature Communications 13.1 (2022): 2991.
https://doi.org/10.1038/s41467-022-30687-9
[2] Stefan Grimme, Jens Antony, Stephan Ehrlich, Helge Krieg. “A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu” J. Chem. Phys. 132, 154104 (2010).
https://aip.scitation.org/doi/10.1063/1.3382344
[3] Stefan Grimme, Stephan Ehrlich, Lars Goerigk. “Effect of the damping function in dispersion corrected density functional theory” Comp. Chem. 32, 7, 1456-1465 (2011).
https://onlinelibrary.wiley.com/doi/abs/10.1002/jcc.21759
[4] “Materials Project” https://materialsproject.org/
[5] “Crystallography Open Database” https://www.crystallography.net/cod/
関連ニュース
-
2026.1.28プレスリリース製品・サービス
-
2025.7.16プレスリリース企業・経営製品・サービス
-
2025.2.17製品・サービス