PFP v4 Validation
Overview
Since the release of Matlantis in July 2021, PFP (Preferred Potential), the core neural network potential (NNP) technology, has been updated about once every six months, and the latest version, v4, is available as of August 2023. Here, we introduce the validation results of the latest version, v4, in comparison to v3.
Method
Density functional theory (DFT) calculations were performed for comparison using VASP 5.4.4. These calculations were subject to the same computational conditions as during the generation of PFP training data and used the PBE functional and the PAW (Projector Augmented Wave) method. For more information, please refer to the PFP paper [1]. Note that starting from PFP v2, we provide a calculation mode without the Hubbard correction, and this validation is performed using this mode. Therefore, Hubbard correction is also not applied in the DFT calculations for fair comparison.
Results
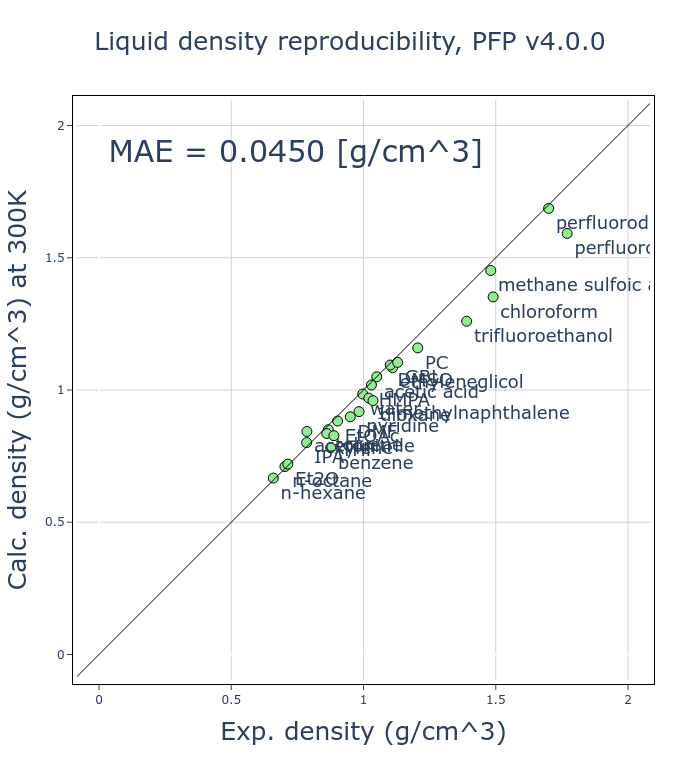
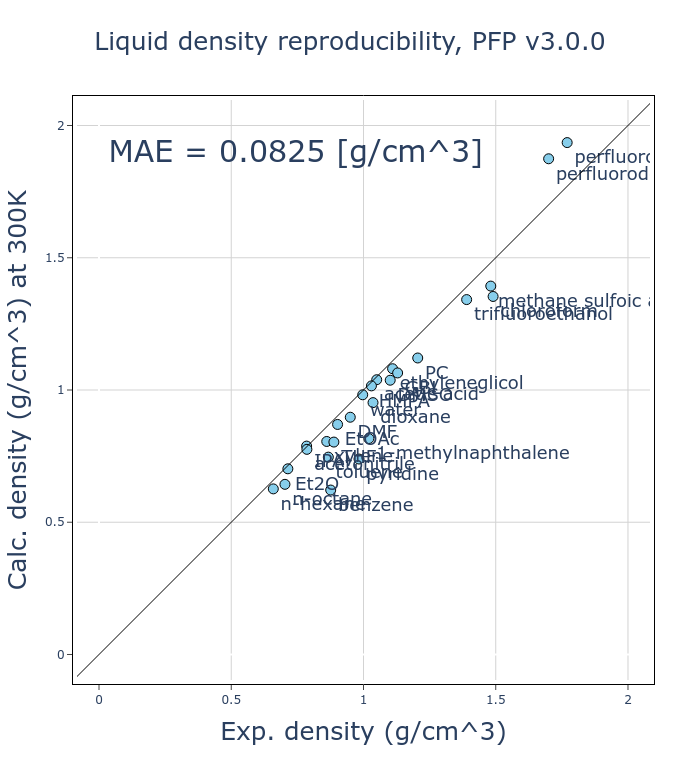
An improvement in v4 is the increased reproducibility of volume and density. To validate this, we have tested the reproducibility of the density of liquids for 26 different organic molecules by comparing them to experimental values. For each organic molecule, molecular dynamics simulations using an NPT ensemble at 300 K and 1 atm were conducted using PFP, using a calculation mode which adds the D3 dispersion correction developed by Grimme et al. [2, 3] to calculate the average density.
The mean absolute error (MAE) of v4 has been reduced to about half that of v3, a significant improvement. As the liquid density of organic molecules is a fundamental physical property, we believe this improvement is of great significance.
The liquid density of organic molecules depends on intermolecular interactions, which are considerably smaller than intramolecular interactions. While classical MD potentials treat intra- and intermolecular interactions as separate terms, PFP and other NNPs treat them in the same terms. Despite the challenges of reproducing liquid density in general-purpose NNPs, because of the need to reproduce various states, we were able to obtain improvements through various innovations.
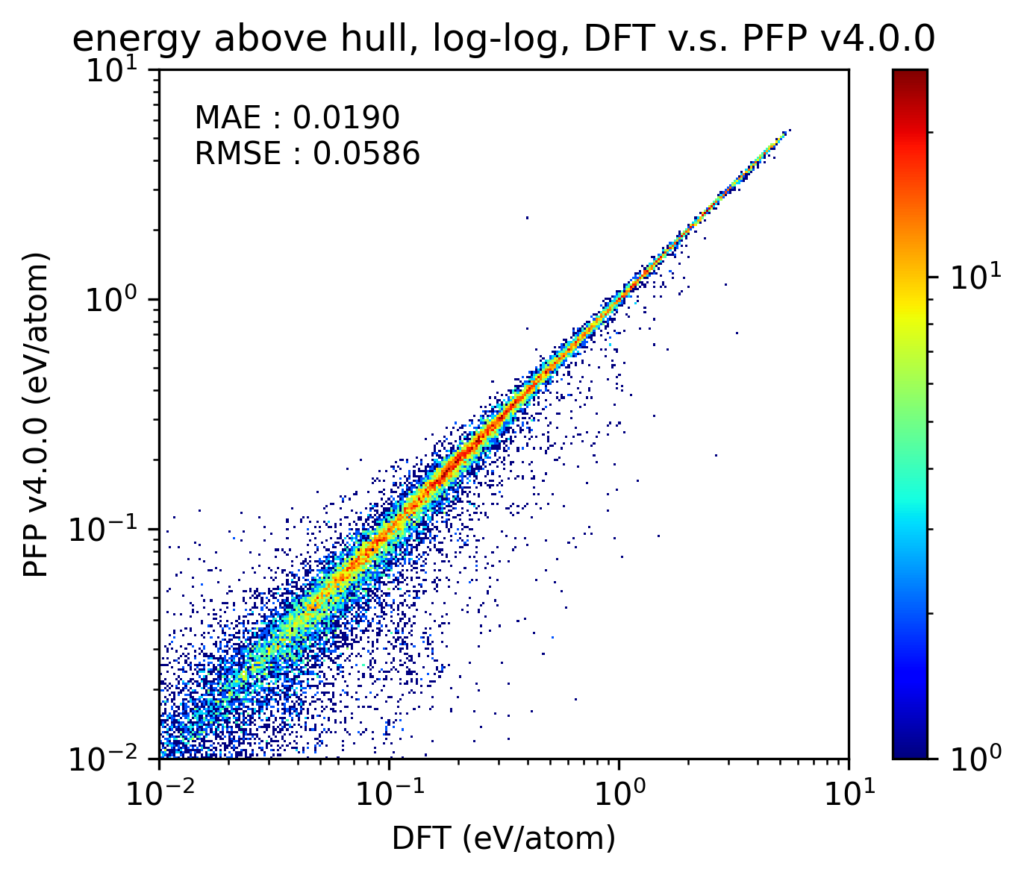
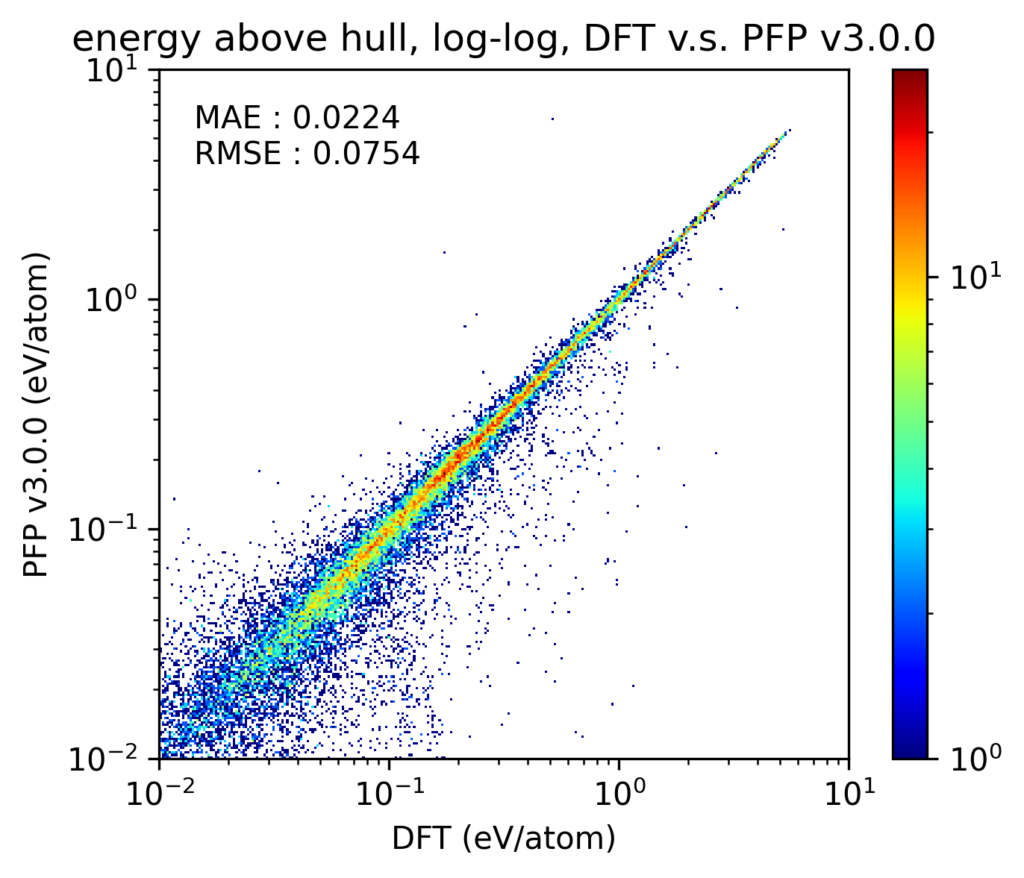
In v4, the reproducibility of compositional phase diagrams has also been improved. In this section, we will consider phase diagrams for different composition ratios at zero temperature and pressure.
To investigate the reproducibility of phase diagrams, we compared the energy difference above the convex hull (Ehull) of the corresponding compositional phase diagram. We considered structures present in the Materials Project [4] containing 1, 2, and 3 unique elements; moreover, we restricted our scope to only structures containing the 72 elements supported by PFP. These crystal structures, including lattice constants, are optimized by both DFT calculations and PFP for comparison. Note that many of these crystal structures were also included in the PFP training dataset.
The results are shown in the y-y plot. Note that the y-y plot excludes structures that are on the convex hull in the DFT calculation. Note that both the axes and the color scale are in the log scale.
In both v4 and v3, most of the structures are on the diagonal of the y-y plot, which shows that the DFT calculation results are reproduced without failure for both large and small Ehull structures. Also, although it is difficult to visually discern from the plot, there is approximately a 20% improvement in MAE for v4 compared to v3.
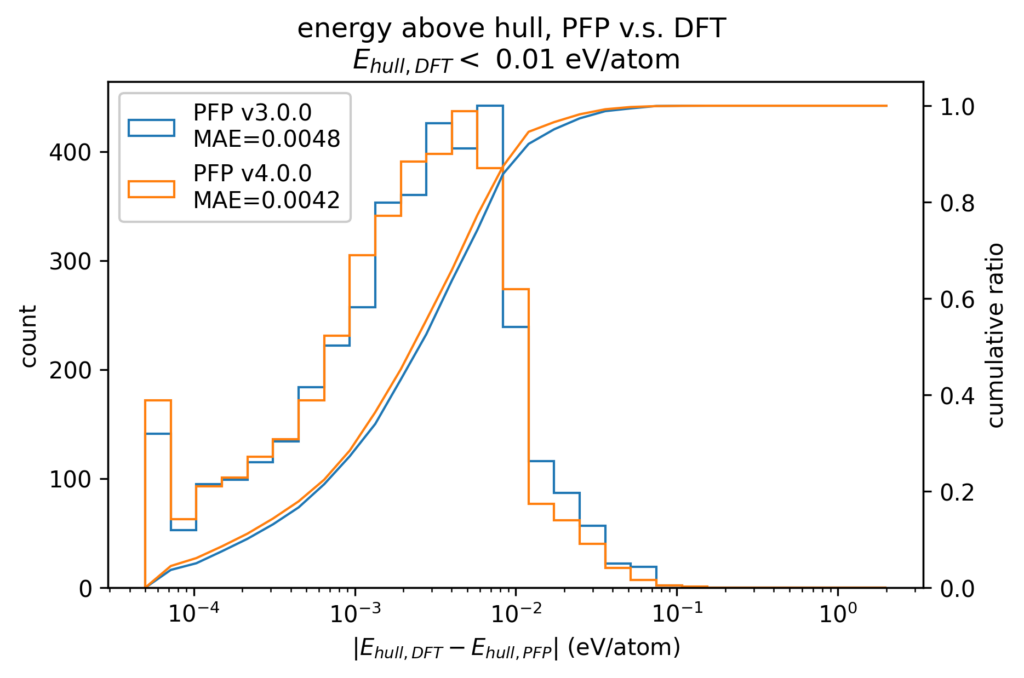
When evaluating the stability of crystal structures in materials discovery, structures near the convex hull, i.e., crystal structures with small Ehull, are required to be able to calculate Ehull with smaller errors.
The following figure shows a histogram of the absolute value of the error of Ehull between the DFT calculation results and PFP results, focusing on structures with Ehull less than 0.01 eV/atom in the DFT calculation. The MAE in v4 is 0.0042 eV/atom, which is about 20% better than v3.
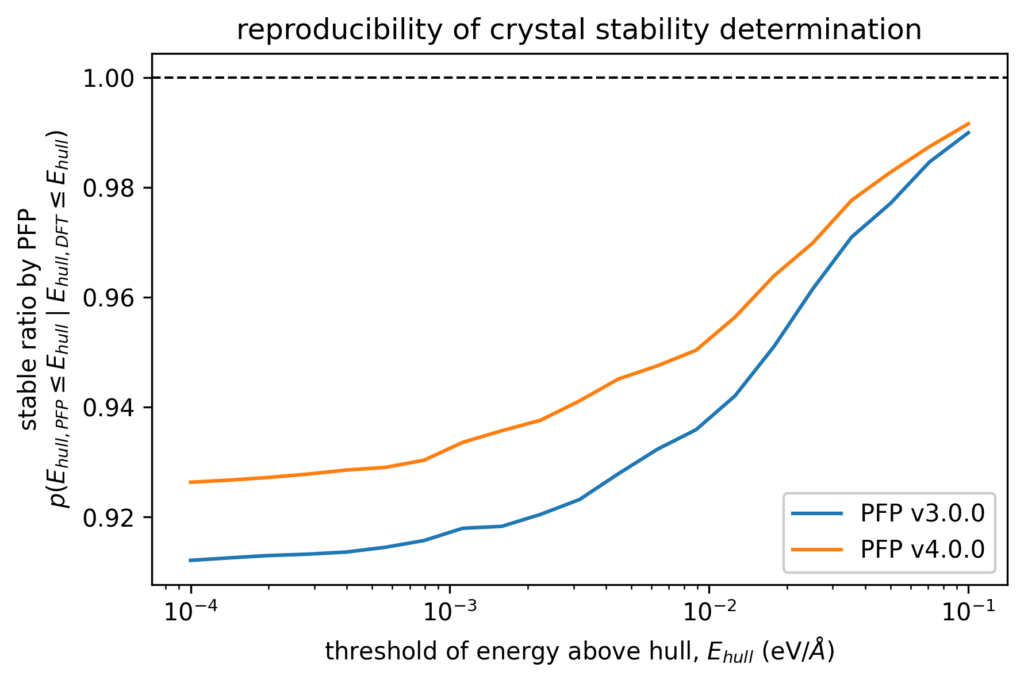
Looking at the case for determining the stability of a crystal structure, we tested whether a crystal structure determined to be stable by DFT calculation is also considered to be stable by PFP. More specifically, we considered setting a threshold value of Ehull to determine stability. Among crystal structures whose Ehull is less than this threshold value when computed with DFT, we computed the fraction of crystal structures whose Ehull was also within the threshold when computed with PFP. This fraction is one if Ehull with PFP are below the threshold for all structures whose Ehull with DFT are below the threshold. The plot of this fraction with respect to the threshold value is shown in the figure below.
In the case of 0.005 eV/atom, which is the threshold often used in DFT calculations to find crystal structures, the value in v3 was 0.930, while in v4, it improved to 0.946. In other words, the number of cases where a structure judged stable by the DFT calculation is judged unstable by PFP has been reduced from about 7.0% in v3.0.0 to about 5.4% in v4.0.0, about 3/4 of that in v3.0.0.
With these improvements, we believe that PFP v4 has reached a level where it can be used for crystal structure searches.
Summary
We have presented validation results of PFP v4, which show greatly improved reproducibility of the liquid density of organic molecules compared to v3. as well as improved reproducibility of the phase diagram. We believe that PFP has reached a level where it can be used for crystal structure search.
Details
We believe that the improved reproducibility of liquid density and phase diagram contributes to the improved reproducibility of PFP energy, force, and density for various structures. Below are the validation results for crystal structures contained in the Crystal Open Database (COD) [5] for structures composed of the 72 elements supported by PFP not included in the PFP training dataset. However, it is possible that similar structures were included in the structures obtained from the Materials Project, which are included in the training dataset.
After structure optimization of these crystal structures with DFT calculations, we plotted the energies and forces of the structures with small displacements in atomic positions. The energy is divided by the number of atoms, with the energy of a single atom in vacuum being zero. Forces are the XYZ components of the force acting on each atom independently. Note that the color scale is a log scale, with one red point being 103 (left) or 107 (right) times the value of one blue point.
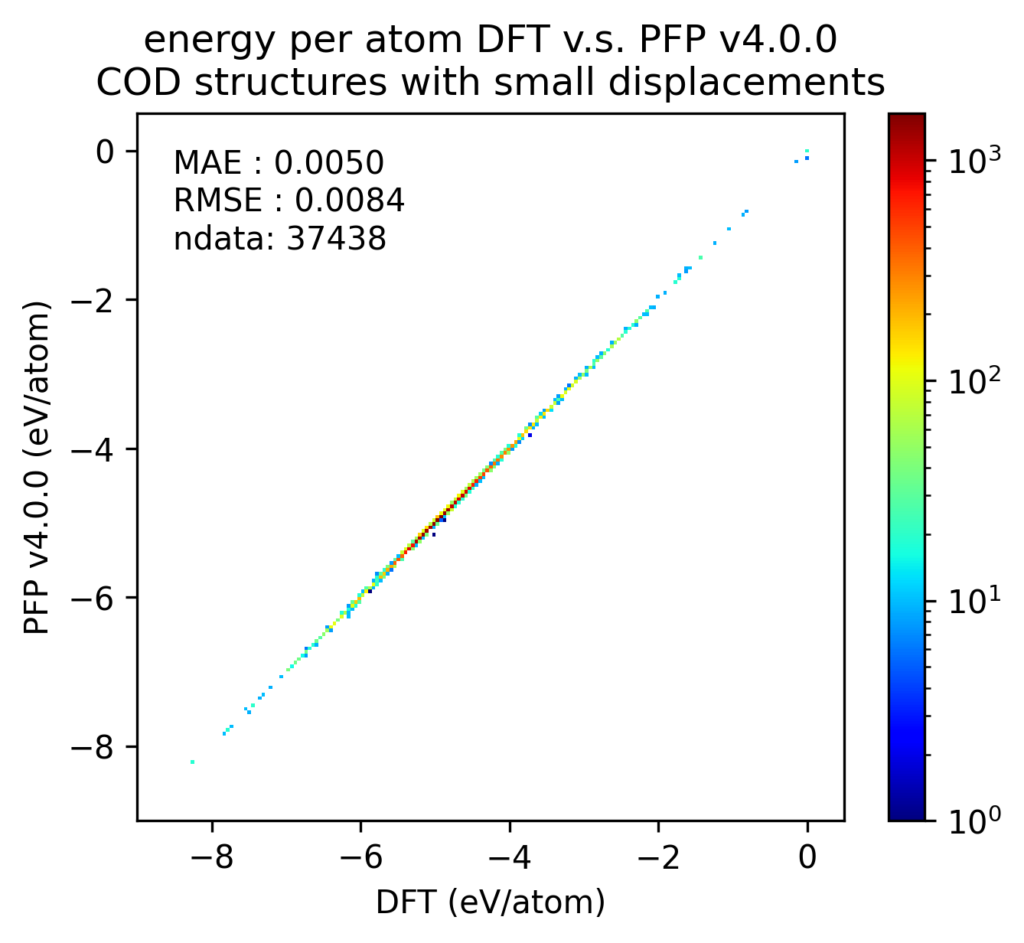
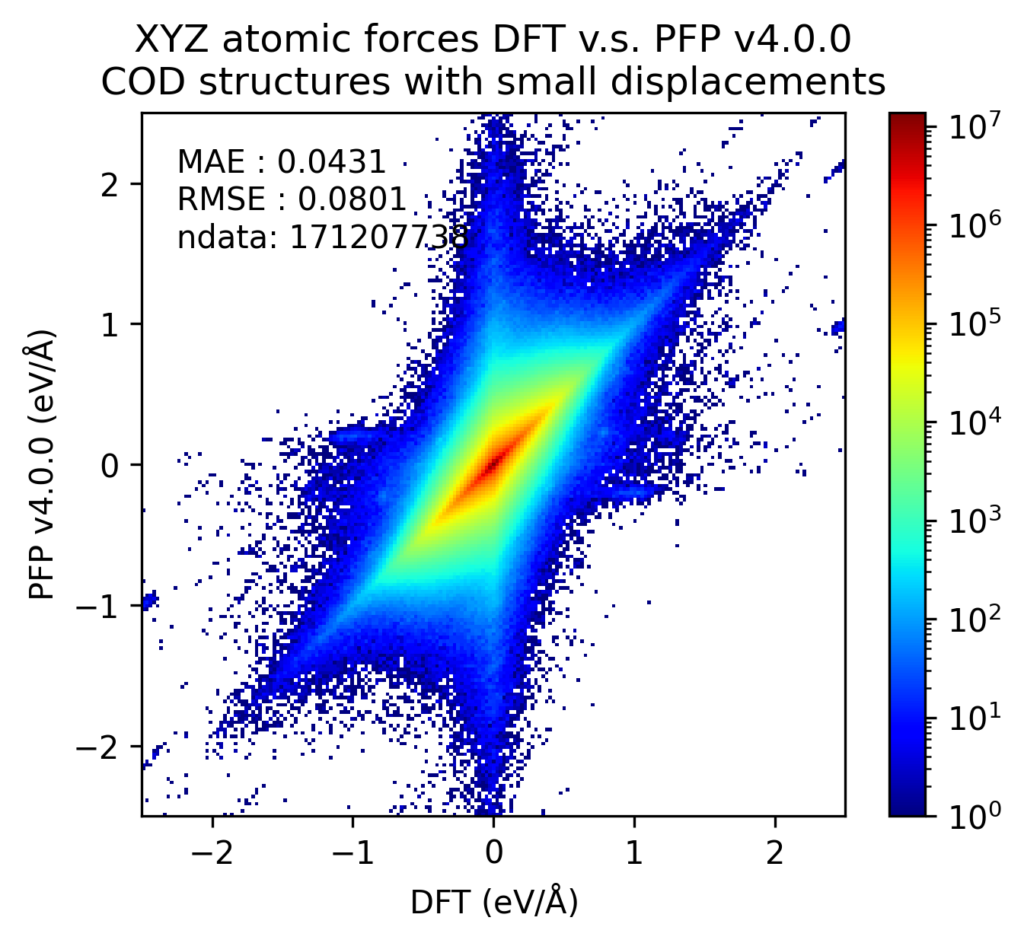
The below histograms show the error between the value in the DFT calculation and the value in the PFP. The forces do not evaluate the XYZ components independently, but rather take the L2 norm (length) of the vector difference. Both of these are improved in v4 from v3.
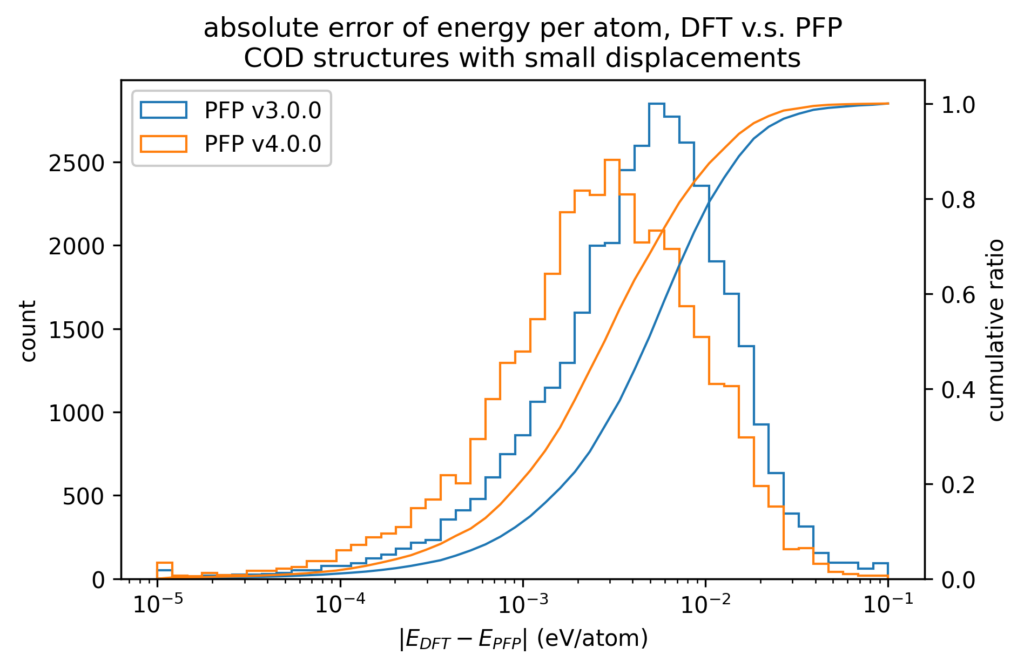
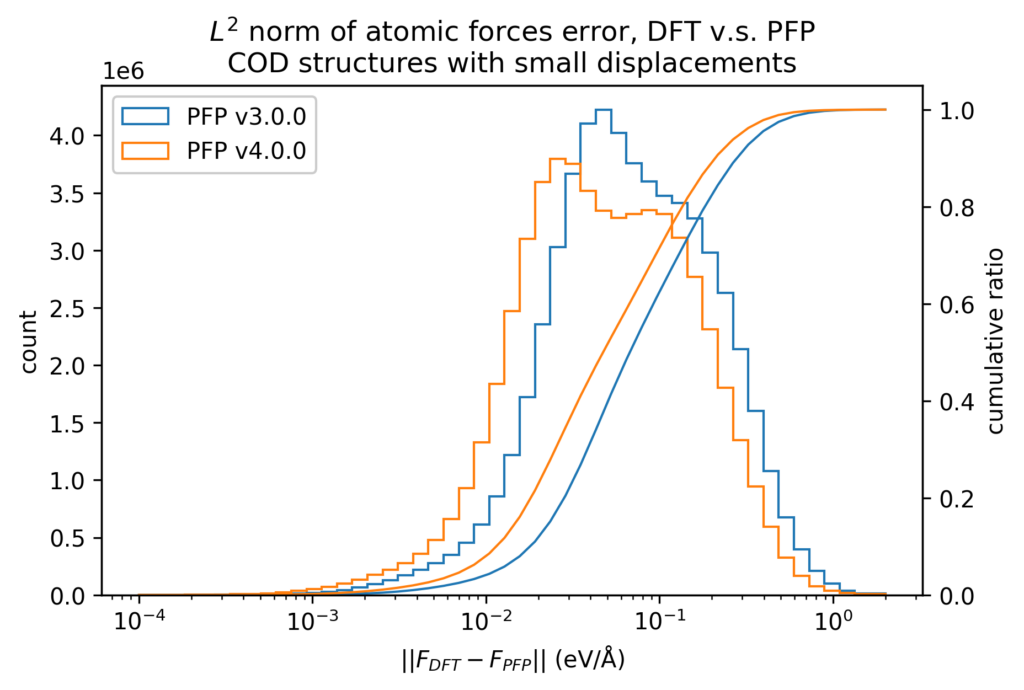
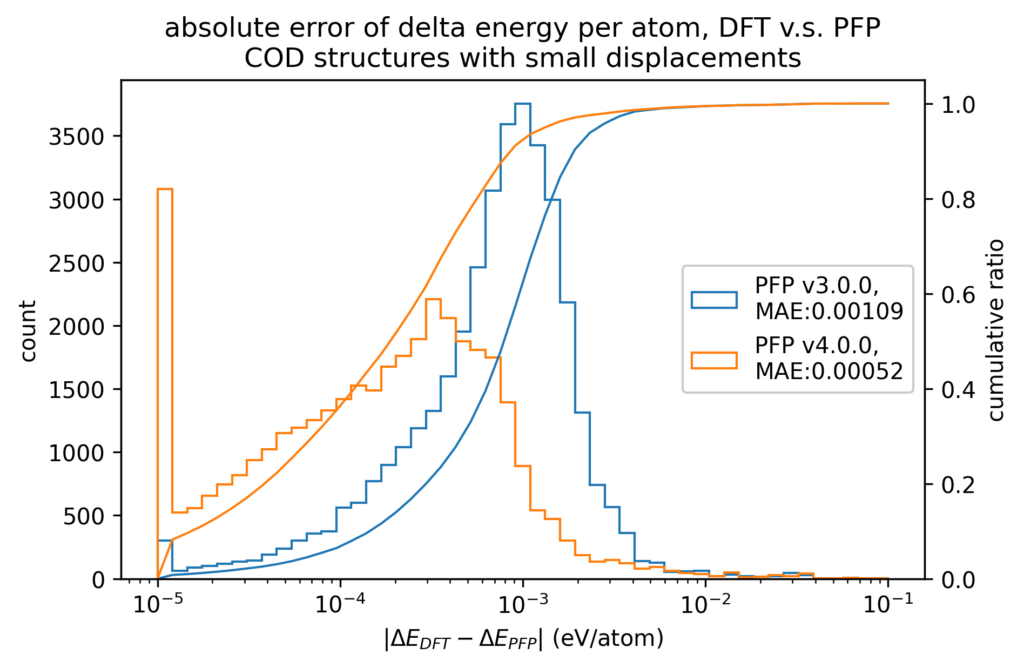
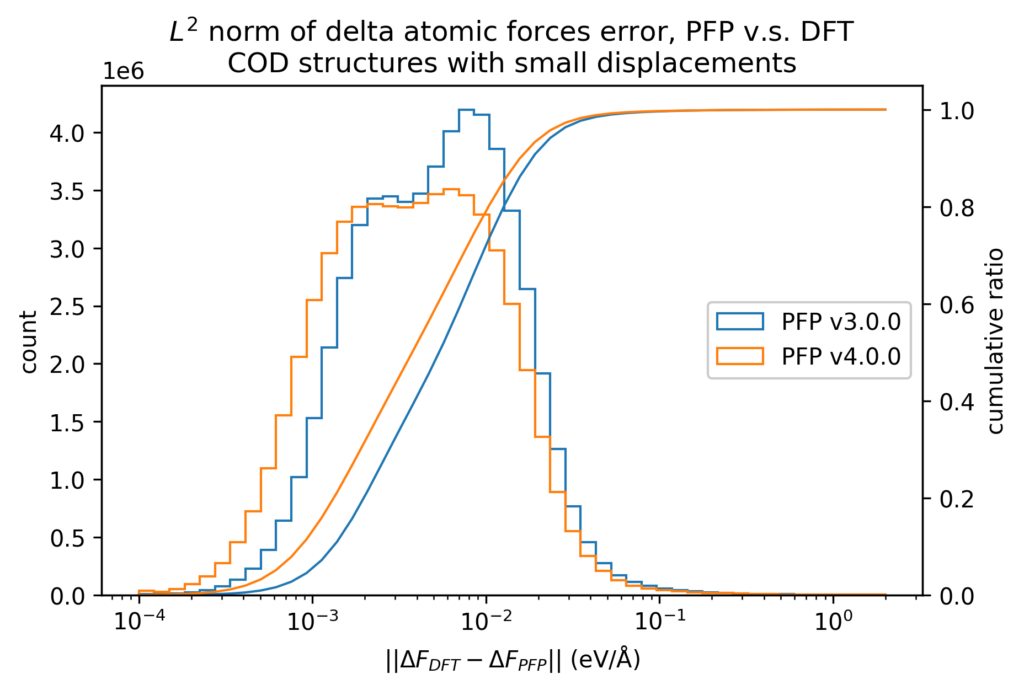
We also compare the changes in energy and force before and after applying small displacements to the atomic positions between the DFT calculation and PFP. The error in the change in energy and force due to small displacements is more than one order of magnitude smaller than the error in energy and force itself. Therefore, physical properties for which local energy surfaces are important, such as force constant, can be expected to be calculated more accurately.
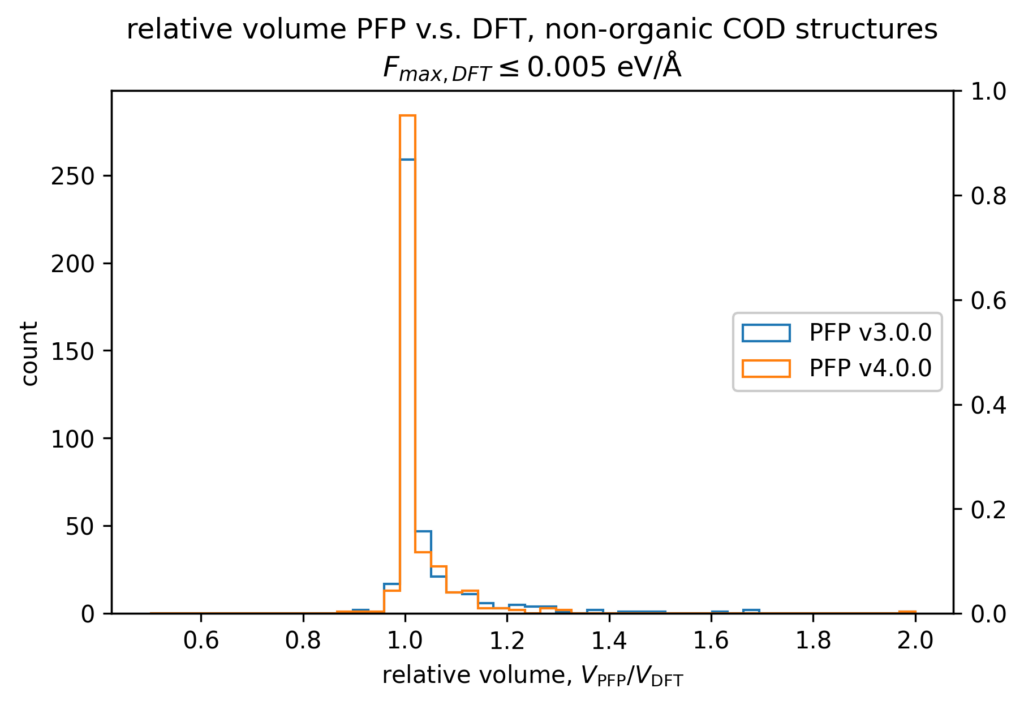
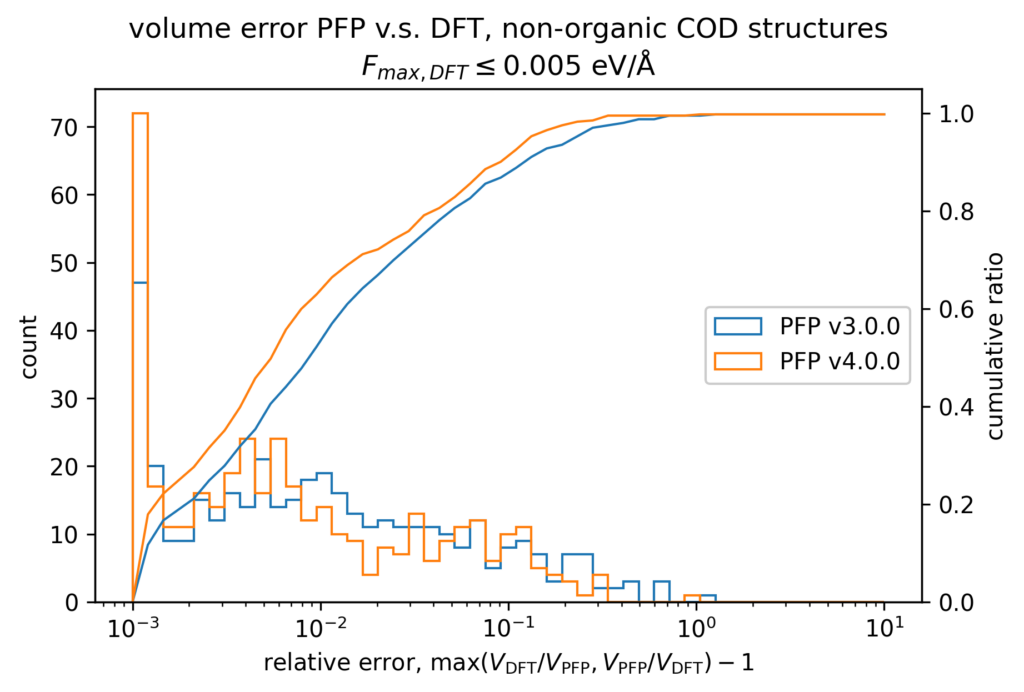
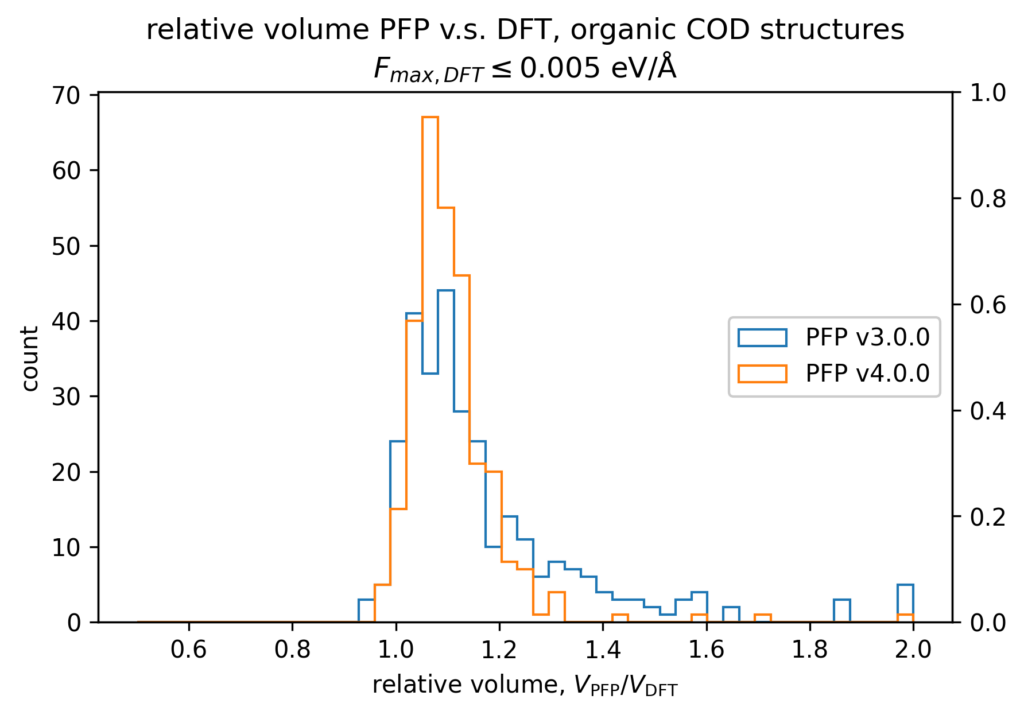
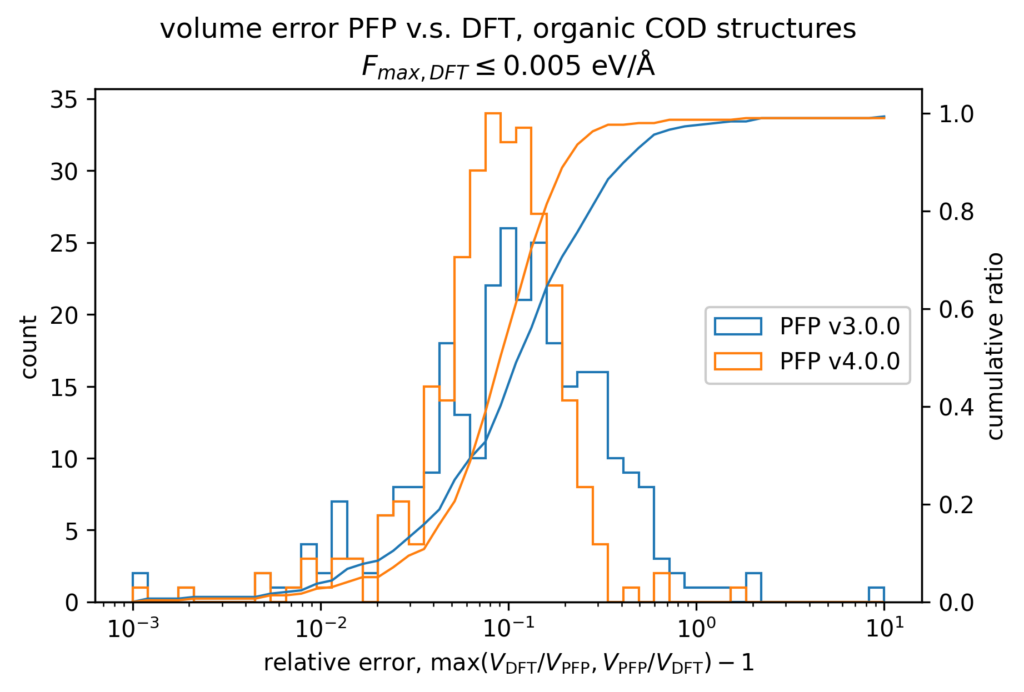
The volume reproducibility is shown below, with the structure optimized so that the force is less than 0.005 eV/Å for the DFT and PFP calculations, respectively. The structures consisting only of H, C, N, O, P, S F, Cl, Br, and I are classified as organic and others as non-organic and compared separately in our validations.
While the volume reproducibility of non-organic structures looks promising, we believe that there is room for further improvement in the volume reproducibility of the organic structures. We believe it is more difficult to reproduce the volume of organic crystals more precisely than inorganic crystals because of their large elastic modulus and the weak force of intermolecular interactions. Additionally, it seems that volume tends to be overestimated by about 5% for organic structures, which we consider to be an issue that needs to be improved.
Acknowledgement
The latest version of Matlantis’s neural network potential, PFP v4, was developed using the National Institute of Advanced Industrial Science and Technology’s AI Bridging Cloud Infrastructure (ABCI) as well as PFN’s in-house supercomputers.
References
[1] Takamoto, So, et al. “Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements.” Nature Communications 13.1 (2022): 2991.
https://doi.org/10.1038/s41467-022-30687-9
[2] Stefan Grimme, Jens Antony, Stephan Ehrlich, Helge Krieg. “A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu” J. Chem. Phys. 132, 154104 (2010).
https://aip.scitation.org/doi/10.1063/1.3382344
[3] Stefan Grimme, Stephan Ehrlich, Lars Goerigk. “Effect of the damping function in dispersion corrected density functional theory” Comp. Chem. 32, 7, 1456-1465 (2011).
https://onlinelibrary.wiley.com/doi/abs/10.1002/jcc.21759
[4] “Materials Project” https://materialsproject.org/
[5] “Crystallography Open Database” https://www.crystallography.net/cod/
