はじめに#
PostPhononBandFeature
では、 ForceConstantFeature で計算された力定数からフォノン分散を求めることができます。
計算手法#
ForceConstantFeature ( 計算手法 参照)では、 結晶構造のスーパーセルから力定数を計算する方法を紹介しました。
primitiveセルに (N) 原子を含む結晶では、力定数は (3N times 3N times M) のテンソルになります
( (M) : 力定数の計算に用いられたprimitive cell の繰り返しの回数)。
フォノン分散は力定数を解析することで求めることができます。
フォノン振動数#
まず、与えられた波数 (vec{q}) に対するフォノン振動数が計算されます。
力定数を用いて、次の式から dynamical matrix を計算します。
ここで登場するベクトル (vec{q}) は波数と呼ばれ、dynamical matrixは波数に依存します。
dynamical matrix の次元は (3N times 3N) となります。
この行列を対角化することで、 (3N) の固有値と固有ベクトルを得ることができます。
固有値は波数 (vec{q}) でのフォノン振動数であり、固有ベクトルはそのフォノンモードでの原子の変位に相当します。
ブリルアンゾーン#
フォノン計算において波数 (vec{q}) が導入されました。波数は物理的には振動モードの伝播方向を表しており、これは第一ブリルアンゾーンに限定されます。
matlantis-features では、入力された結晶の第一ブリルアンゾーンを可視化する機能を提供しています。
PostPhononBandFeature 実行後、
PostPhononBandFeatureResult がアウトプットされます。
visual_k_path 関数を用いることで、第一ブリルアンゾーンを可視化できます。
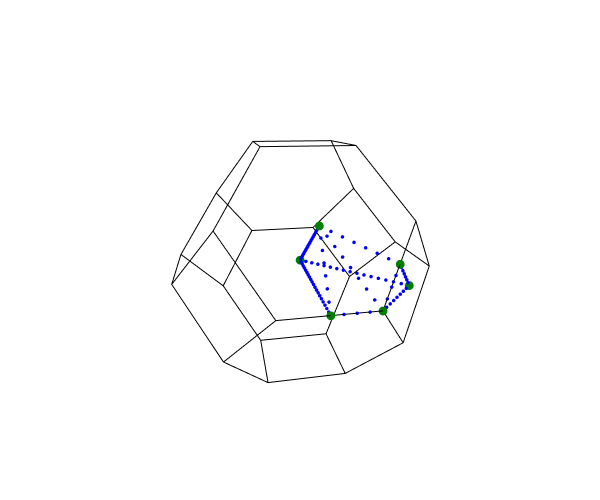
visual_k_path 関数を用いて描画されたシリコン結晶の第一ブリルアンゾーン。#
ブリルアンゾーン中のいくつかの高い対称性を持つ地点はspecial k-pointと呼ばれます
(このページでは波数を表すのに (q) を用いていますが、電子のバンド理論との対応のためあえてk-pointと呼ぶことにします。)
上の図では、全special k-pointが緑色にマークされています。
各ブラべー格子には固有ののspecial k-pointがあり、 (Gamma) や (K) のような文字でラベル付けされています。例えば、FCC格子のブリルアンゾーンには (Gamma, K, W, X, U, L) の6つのspecial k-pointがあります。
k-point path#
全フォノン振動数を取得するためには、ブリルアンゾーン内のすべての (vec q) 点について計算を行う必要があります。しかし、実際にはいくつかの対称性の高い経路上の (vec q) 点を代表的に用いることがよくあります。
上の図で表示されている経路はspecial k-pointを繋いでいます。フォノン振動数を対象性の高い経路(k-point path)に沿ってプロットしたものを、フォノン分散と呼びます。
k-point path には標準的に使われる経路があります (後述しますが、任意に定義することもできます)。
たとえば、FCC格子では
(Gamma rightarrow X rightarrow W rightarrow K rightarrow Gamma rightarrow L rightarrow U rightarrow W rightarrow L rightarrow K)
および
(U rightarrow X)
がよく用いられます。
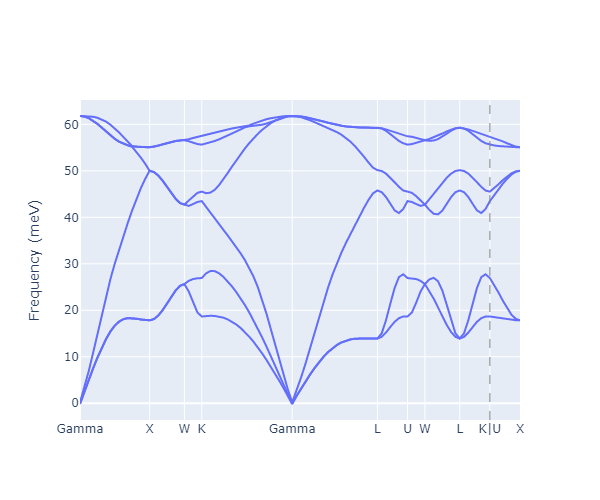
標準的に用いられるk-point pathに沿った、シリコン結晶のフォノン分散。#
フォノン分散#
設定されたk-point path上でフォノン振動数を計算することで、上図にプロットされたようなフォノン分散を得ることができます。
1つの k-pointには (3N) 個の振動数があるため、フォノン分散には (3N) 本の枝分かれがあります。しかし、特定の (vec{q}) 点では枝分かれが重なることがあります。
PostPhononBandFeature を用いてフォノン分散を計算するコードの例です:
# The variable "force_constant" is obtained from `ForceConstantFeature`.
# Please see `Matlantis-features: Phonon` on the launcher page.
from matlantis_features.features.phonon import PostPhononBandFeature
band = PostPhononBandFeature()
band_results = band(
force_constant,
labels = ['Gamma', 'X', 'W', 'K', 'Gamma', 'L', 'U', 'W', 'L', 'K', '|', 'U', 'X'],
special_kpts = np.array([
[0.000, 0.000, 0.000], # Gamma
[0.500, 0.000, 0.500], # X
[0.500, 0.250, 0.750], # W
[0.375, 0.375, 0.750], # K
[0.000, 0.000, 0.000], # Gamma
[0.500, 0.500, 0.500], # L
[0.625, 0.250, 0.625], # U
[0.500, 0.250, 0.750], # W
[0.500, 0.500, 0.500], # L
[0.375, 0.375, 0.75 ], # K
[0.625, 0.250, 0.625], # U
[0.500, 0.000, 0.500], # X
]),
)
# visualize of Brillouin zone and k-point path
brillouin = band_results.visual_k_path()
# visualize of Phonon dispersion
dispersion = band_results.plot()
Tips#
-
標準的なk-point path以外の経路を用いたい場合、
special_kpts引数にk-pointのラベルと座標を格納したリストを渡すことで独自のk-point pathを設定することができます。 -
labelsとspecial_kptsのどちらも定義されていない場合、デフォルトのk-point pathが使用されます。その場合、style='ase'とすればASE方式、style='phonondb'とすれば Phonon Database 方式のk-point pathを参照します。 -
k-point path を定義する際、いくつかの不連続な経路を組み合わせることができます。各経路を
|で区切ってください。
Examples#
Launcherからアクセスできる Matlantis-features: Phonon および Matlantis-features: Phonon Advanced Usage をご覧ください。