Density functional theory (DFT) is a theory that attempts to understand the behavior of atoms and electrons based on the principles of quantum mechanics. Calculations based on DFT formulas (DFT calculations) can provide information on materials at the atomic level, and are therefore used to calculate various physical properties and elucidate various phenomena.
Due to improved accessibility resulting from advances in both computational hardware and software, and growing recognition due to an increase in examples, there has been an increase in reports of applied calculations using DFT calculations in the field of materials development. Furthermore, in recent years, there have been cases where DFT calculations are used to generate data under consistent computational conditions for materials informatics (MI).
This article is aimed at beginners and explains the theoretical background of DFT and the phenomena and physical properties that can be calculated. Since rigor is sacrificed in favor of simplicity, those who wish to learn more should refer to specialized books [1, 2].
What is Density Functional Theory (DFT)?
Density Functional Theory (DFT) is a theory that attempts to understand the behavior of atoms and electrons based on the principles of quantum mechanics. According to DFT, if the electron density for a given structure such as a crystal or molecule is known, the corresponding energy and electronic state can be uniquely determined. In density functional theory, density refers to "electron density," and functional is a technical term that means "function of function." Electron density ρ is a function ρ (r) determined by electron position r, and according to DFT, energy E is determined by electron density ρ (r), so energy is a function of electron density, i.e., a functional (= E [ρ (r)]).
If we know the energy of a system, we can quantitatively compare the stability of various crystal and molecular structures. Furthermore, the electronic state can provide important information related to physical properties and reactivity, such as band gaps, molecular orbitals, and atomic net charges.
The currently mainstream calculation method is to numerically calculate the Kohn-Sham equation using a dedicated program and computer under the input structure and calculation conditions (DFT calculation). Using the information obtained from DFT calculations, numerous calculation examples have been reported, from basic to applied.
The role of DFT in computational chemistry
Generally, "computational chemistry" refers to the field and methodology of theoretical analysis and prediction by mathematically modeling physical and chemical phenomena and simulating them on a computer. The physical properties and reactions of materials are particularly dominated by the state of atoms and electrons, and calculations based on quantum chemistry are necessary to theoretically handle this scale. DFT is one of the theories based on quantum chemistry, and is considered to be on the same level as wave function theory (Schrödinger equation).
Figure 1 shows the spatial and temporal domains targeted by DFT calculations. The real-world domain that DFT calculations can cover is on the order of nm and ns, and application to systems with sizes greater than this is virtually impossible. Therefore, if you want to examine physical properties or phenomena over larger or longer time scales, you must use a different calculation method appropriate for the scale.
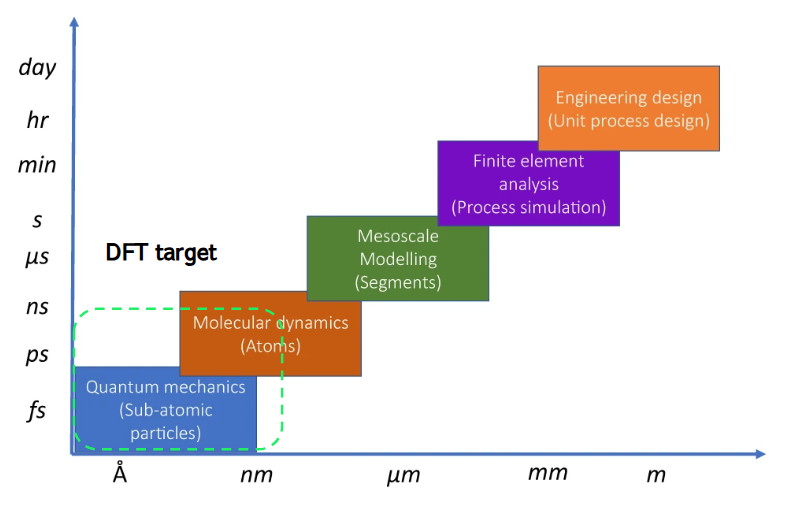
Figure 1. The length and time scale domains covered by computational chemistry and the target domain for DFT calculations. (Adapted from Fig. 1 in Ref. [3]. Licensed under CC BY 4.0).
In what fields is DFT calculation used?
DFT calculations are effective for calculating various physical properties involving electrons and atoms, and thanks to advances in computational hardware and software, the number of reported application calculations is increasing year by year. Figure 2 shows the results of a cluster analysis of the contents of papers in the materials field (approximately 100,000 papers from 2010 to 2023). Technologies important for realizing a sustainable society, such as batteries, catalysts, hydrogen storage materials, and optical materials, are located near DFT. This 2D map suggests that DFT calculations are widely used in research and development in these fields.
The number of papers using DFT calculations is currently on the rise, and it is expected to continue to play an important role in the development of cutting-edge materials. Patents and applications using DFT calculations have also been filed, making it an important elemental technology that has a significant impact on a company's development speed and competitiveness (for details, please refer to the research report published on our website).
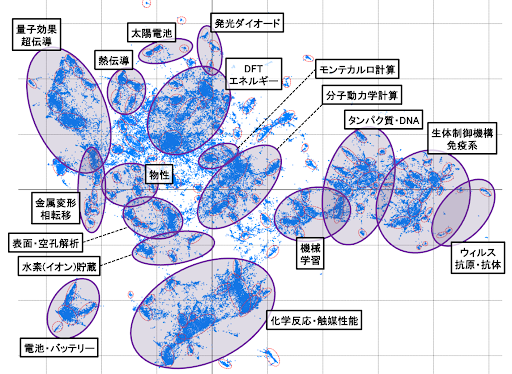
Figure 2. 2D map of cluster analysis of approximately 100,000 academic papers in the materials field.
Physical properties and phenomena that can be calculated using DFT
As explained at the beginning, DFT calculations provide the energy and electronic state of a system. Using this basic information, various physical properties and phenomena can be calculated.
In DFT calculations, the calculation method and the physical properties that can be calculated vary depending on the material system being studied. Here, we consider "solid/periodic systems" and "molecular systems" as rough classifications of systems. "Solid/periodic systems" refers to solids and surfaces such as metals and semiconductors, and condensed structures such as amorphous and liquid. By assuming that the input structure is arranged periodically (periodic boundary conditions), calculations for infinitely large systems are possible. If you want to calculate the electronic state and physical properties of an aggregate of atoms and molecules, you use calculation methods for solid/periodic systems.
"Molecular systems" literally refer to molecules such as water (H₂O) and methane (CH₄), as well as clusters of these molecules that interact with one another. Calculations are usually performed in a vacuum, but calculations that take solvent effects into account are also possible. Calculation methods for molecular systems are suitable when you want to calculate the properties of individual molecules or reactions in homogeneous systems with high accuracy.
Below we introduce some of the physical properties and phenomena that can be calculated using DFT calculations.
Structural Properties
DFT can calculate not only the energy for the input structure but also the forces acting on atoms. By calculating structural changes so that these forces become zero, it is possible to obtain a physically realistic stable structure (structural optimization). Electronic states and static physical properties are generally discussed using the structure after structural optimization. Please note that structural optimization is calculated under 0 K conditions.
For periodic structures such as crystals, calculations are performed by setting a repeating unit cell and applying periodic boundary conditions. In this case, not only the atomic positions but also the lattice constants can be optimized as structural changes. The stable structures obtained from calculations can be directly compared with experimental structures, for example, spectroscopic data such as X-ray diffraction.
Elastic constants are an example of calculations of physical properties related to structure. By calculating the change in energy for a small atomic displacement, it is possible to obtain Young's modulus, bulk modulus, shear modulus, and other properties. These elastic constants are important physical properties for structural materials and mechanical parts, and are an example of how macroscopic physical properties can be obtained from calculations of microscopic systems.
Band structure and molecular orbitals
DFT can obtain the band structure and molecular orbitals corresponding to the electronic state in a material. For solids and periodic systems, the band gap can be calculated from the energies of the conduction band and valence band. Since the band gap is directly related to electrical conductivity and optical properties, it is essential information for the development of materials such as semiconductors.
For molecules, the energy levels and spatial distribution of molecular orbitals can be calculated. In particular, the energy levels of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are related to chemical reactions, optical absorption, and electron transport properties. This information provides very useful insights, for example, when discussing the stability of polymer materials.
DFT also allows us to convert information about these orbitals to calculate the net charge on atoms. Based on the charge distribution in a system, we can discuss polarity and reactivity.
Thermal properties/transport properties
For solids and periodic systems, specific heat, thermal expansion coefficient, thermal conductivity, etc. can be calculated by calculating the dispersion relationship of lattice vibrations (phonons). Similar methods can also be used to calculate thermodynamic quantities such as free energy. These physical properties can be used as indicators of structural changes due to heat to evaluate the material properties for electronic devices.
For molecular systems, molecular vibrational analysis can be calculated (the results can also be visualized as IR spectra). By creating a partition function from vibrational frequencies, thermodynamic quantities such as entropy, specific heat, and free energy can be calculated. This makes it possible to evaluate thermodynamic stability taking into account the effect of finite temperature.
Transport properties such as diffusion coefficients and viscosity can also be calculated using molecular dynamics (MD), a method that tracks the time evolution of atoms at finite temperatures (see also our blog post on MD). Diffusion coefficients, in particular, are often used to evaluate the ionic conductivity of battery-related materials such as solid electrolytes and proton-conducting membranes.
Response properties
In DFT calculations, the response properties of each external field (electric field, magnetic field, light, etc.) can be obtained by calculating the energy change in response to the external field.
Polarizability, permittivity, dielectric loss, and other properties can be calculated as a response to an external electric field. These are important properties for designing materials for capacitors and sensors. In addition, the response to an external magnetic field can be used to calculate the magnetic moment, magnetic susceptibility, and chemical shift of the NMR spectrum of the structure. These properties are used to evaluate materials for permanent magnets and magnetic recording media.
Furthermore, time-dependent DFT (TD-DFT) can be used to calculate the energy and transition probability of electronic excited states in materials responding to light. This information can be used to simulate UV-Vis absorption and emission spectra. Because it can also calculate the energy difference between singlet and triplet excited states, it is often used to search for luminescent molecules for thermally activated delayed fluorescence materials.
Chemical Reactions
DFT can calculate not only stable structures of reactants, intermediates, and products, but also transition state structures that are difficult to analyze experimentally. From the energy difference between the obtained structures, it is possible to calculate the reaction energy and activation energy of the corresponding chemical reaction. Based on this information, an energy profile along the reaction path can be created, allowing for quantitative discussion of the rate-determining step and selectivity of the reaction.
Analysis of chemical reactions is one of the most widely used areas of DFT calculations. Catalytic reactions, in particular, usually involve a large number of complex elementary reactions, making computational analysis of reaction pathways extremely effective.
By changing the structure and composition of the catalyst and creating and analyzing similar energy profiles, it becomes possible to go beyond reaction mechanism analysis and rationally design catalytic reactions.DFT calculations are applied to the development of various catalysts, regardless of whether the catalyst is homogeneous or heterogeneous.
Issues and solutions for DFT calculations
As mentioned in the previous section, DFT calculations are extremely useful for understanding structures and phenomena that cannot be tracked by the human eye in time and space, and for calculating physical properties.
Another advantage of DFT calculations is that you can use the computer as a virtual experimental space to immediately try out ideas for structures, conditions, etc. that come to mind. Because it is a virtual experiment, there is no cost to purchase reagents, it is safe, and there is no need for management or cleanup afterwards (though organizing files and folders is necessary). If calculations can be performed faster than experiments, it would also be possible to theoretically screen materials before experiments.
As mentioned above, DFT calculations are a powerful method with many advantages, but they also have fundamental and practical challenges. Here, we will briefly summarize the challenges of DFT calculations and how to address them.
Computational accuracy and functionals
The ideal form of computational chemistry methods such as DFT is to give results that match experiments. In systems A and B that are in equilibrium at room temperature,an energy difference of just 1.3 kcal mol¹ results in a 10-fold difference in the abundance ratio of each element. To discuss such a difference through calculations,accuracy at the kcal mol¹ level is required (chemical accuracy).
While the existence of solutions is theoretically guaranteed in DFT calculations, a practical issue is that the exact form of the equation (functional) to be solved is not known. Because there is arbitrariness in how this equation is constructed, a wide variety of functionals have been proposed, and the accuracy of the calculation depends on the functional used. High-accuracy functionals are generally constructed by adding terms that represent interactions, which increases the amount of calculation and calculation time. As such, when performing DFT calculations, the functional must be selected taking into consideration the application, accuracy, and calculation cost.
Currently, no universal functionals have been reported that achieve chemical accuracy for any system. However, relative values can often be correlated with experiments, so a realistic compromise is to perform calculations using appropriate functionals while understanding their limitations. Research on DFT functionals is still ongoing at the cutting edge, and progress is being made in developing functionals with higher accuracy.
Computation time and size
DFT calculations use the three-dimensional coordinates of atoms as input, but the calculation is not as simple as simply substituting these values into the Kohn-Sham equation to find the energy and electronic state. In reality, iterative calculations are performed using variables related to the electronic state as parameters, and the converged value is taken as the solution.
In addition to this iterative nature of the calculation, in general DFT, the calculation time increases in proportion to the cube of the number of electrons in the system. Depending on the type of calculation, as the number of atoms increases, a single calculation can take weeks or even months. The limit for the size of a system that can be calculated within a realistic time frame is around 100-200 atoms.
To address these challenges, active efforts are being made in both industry and academia to accelerate DFT calculations by applying machine learning techniques. One of these is the creation of machine learning models that reproduce the results of DFT calculations (machine learning potential). Using this method, it becomes possible to calculate systems at ultra-high speeds with accuracy equivalent to DFT. PFP, which can be used in our product Matlantis, also represents machine learning potential. Machine learning potential makes it possible to calculate systems of sizes that would be impossible to calculate using DFT alone due to the computational time required, and to apply it to high-throughput calculations.
Summary
In this article, we introduced what density functional theory (DFT) is, what calculations it can perform, and its advantages and challenges. As research and development efficiency is required, it is expected that materials development using DFT calculations will become increasingly widespread. DFT is undergoing cutting-edge improvements in both accuracy and speed, and it is anticipated that combining it with AI technology could lead to major breakthroughs.
We hope this article will help beginners understand DFT calculations and computational chemistry. In the next application section, we will introduce reports of applied calculations using DFT, citing papers and patents as examples. If you would like to try the calculations in your own environment right now,Our blog postsorAtomistic Simulation TutorialPlease also refer to the following.
Reference Links
- R. G. Parr and W. Yang (1989). Density-Functional Theory of Atoms and Molecules (Oxford University Press).
- Takao Tsuneda (2012). Fundamentals of Density Functional Theory (Kodansha).
- Choudhary, K., Garrity, K.F., Reid, A.C.E. et al. npj Comput Mater 6, 173 (2020).