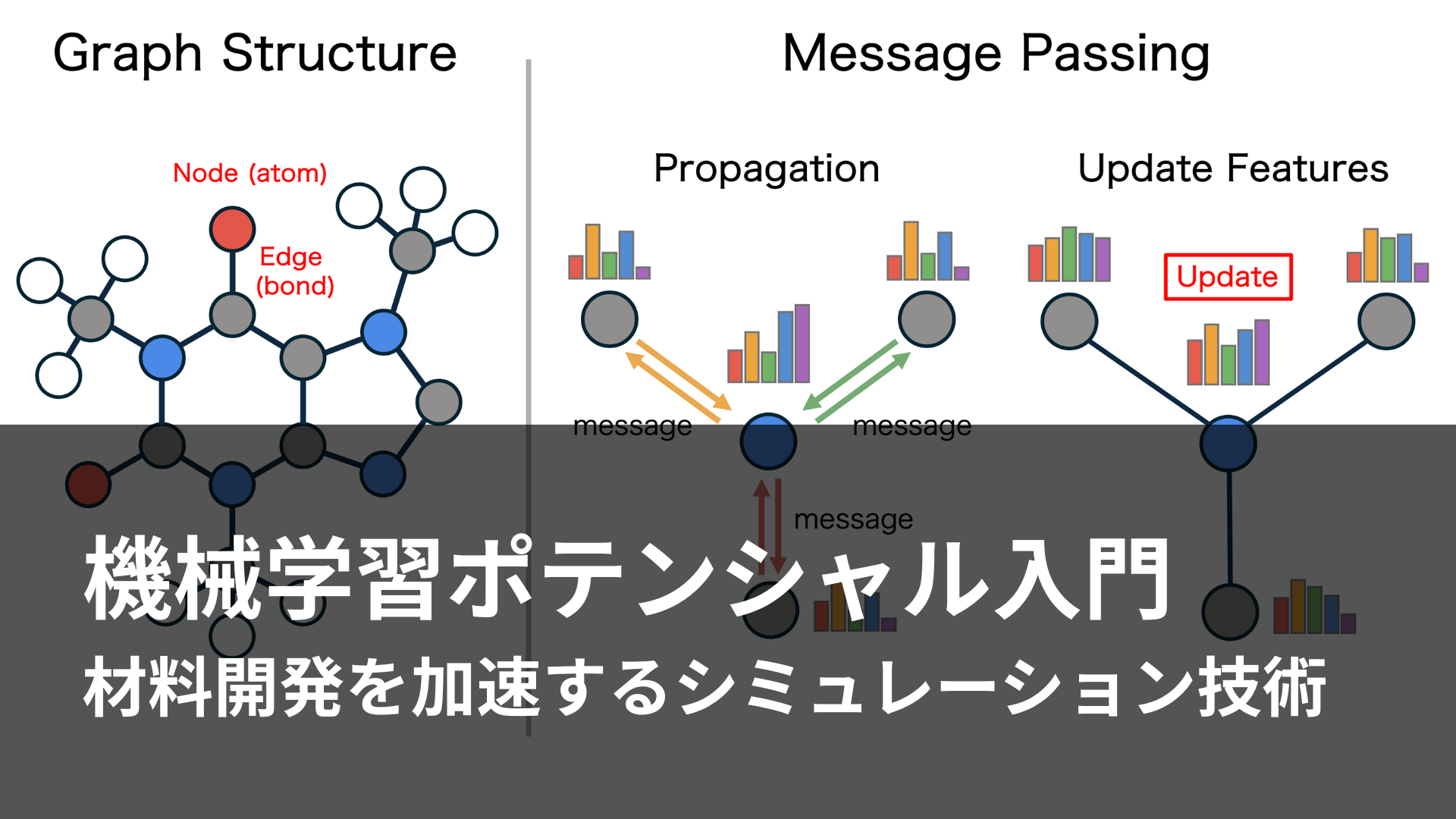
材料研究開発現場で注目される分子動力学シミュレーション
原子や分子の動きをリアルタイムで追跡できる分子動力学シミュレーションは、近年の計算機性能の飛躍的な向上によって、材料、化学、創薬、バイオなど、さまざまな分野の研究開発において不可欠なツールとなっています。
分子動力学シミュレーションは「圧倒的な分解能をもつ顕微鏡」と形容されるように、実験では観測が難しい原子・分子スケールの動きを可視化して、手に取るように現象の背後に潜むメカニズムを理解することを可能にします。実験だけでは得られにくい洞察や合理的な材料設計の指針を研究者にもたらしたり、実験に先立って温度・圧力・組成など多様な条件を仮想的に試行できるため、研究開発プロセス全体の大幅な加速に役立っています。
本記事では、そんな分子動力学シミュレーションを支える要素技術と最新動向を紹介し、それらを活用することでどのような物理現象が解析可能になるのか解説していきます。
分子動力学シミュレーションで何が見えるのか?
分子動力学(MD)シミュレーションでは、原子の座標、速度、エネルギーなどの時系列データが得られます。これらを適切に解析することで、対象となる系の特性を定量的に評価し、有益な知見を抽出することができます。
本章では、MDシミュレーションで広く利用される代表的な計算事例や解析手法を通して、分子動力学シミュレーションがどのように使われているのかを紹介していきます。
(1) 物質の構造特徴を定量化する: 動径分布関数
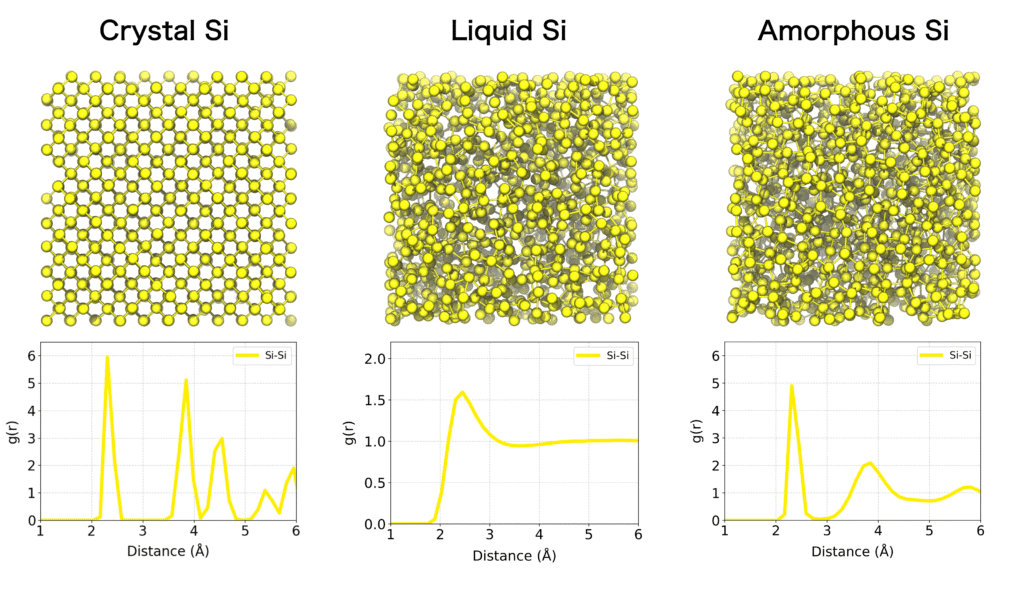
結晶構造とは異なり、液体やアモルファスといった構造は原子レベルの詳細な構造を実験的に観察することは一般的には困難です。分子動力学シミュレーションは、このような系の原子配置や動的挙動を原子レベルで観測できる有力な手段です。
物質の構造的特徴を定量的に評価する手法として動径分布関数(Radial Distribution Function; RDF) が広く利用されています。動径分布関数は、特定の原子を基準に距離rに位置する他の原子の存在分布を示す関数です。結晶構造のような規則構造、あるいは液体やアモルファス系などの不規則ながら局所的秩序を持つような原子・分子集合体の構造的特徴を明らかにするのに有効です。
動径分布関数を用いることで、第一近接原子殻や第二近接原子殻のような特徴的な原子間距離と配位数を定量化できます。動径分布関数の形状は系の相状態を明確に反映します。例えば、結晶性固体では長距離秩序に対応する明瞭かつ周期的なピークが観察されます。一方、液体やアモルファス系では短距離秩序を示す幅広のピークが見られるものの、距離が長くなるにつれて値が1に収束します。また、気相系では原子間相互作用が希薄であるため、RDFはほぼ全域で1に近い値をとります。
動径分布関数はシミュレーションモデルの妥当性を評価したり、実験的に得られた構造データ(例えば、X線や中性子回折の構造因子)との比較において重要な役割を果たします。液体やガラス構造、溶媒和構造、界面構造の解析など、多様な材料に対して幅広く活用されています。
(2) イオンや分子の移動のしやすさを定量化する: 拡散係数
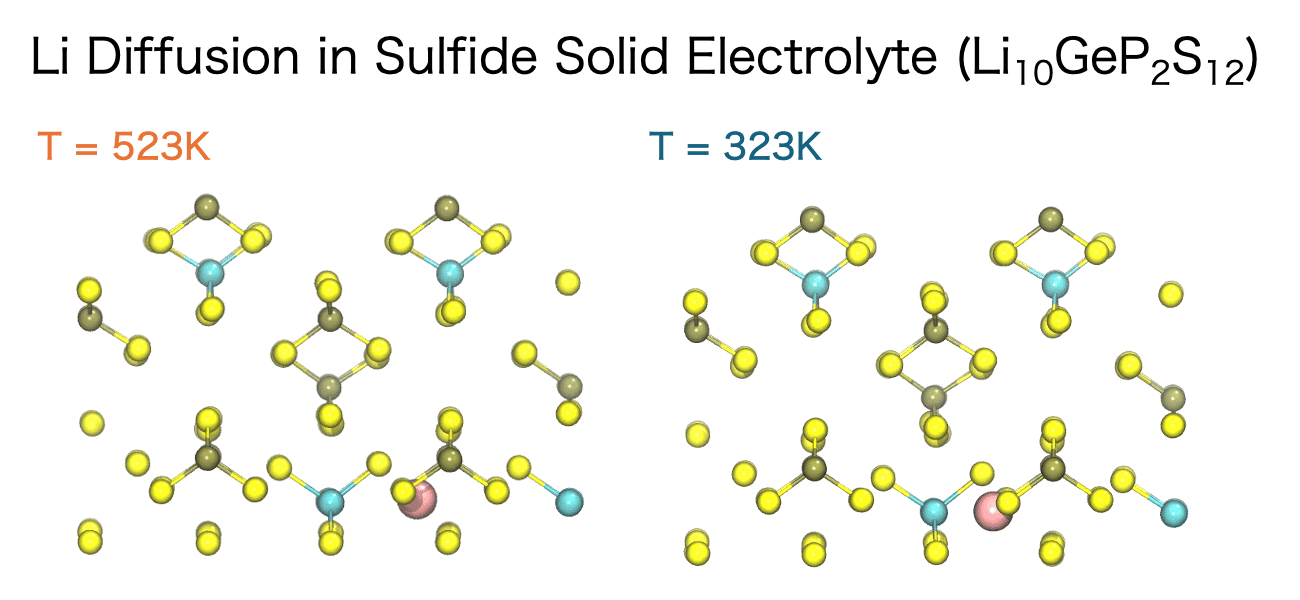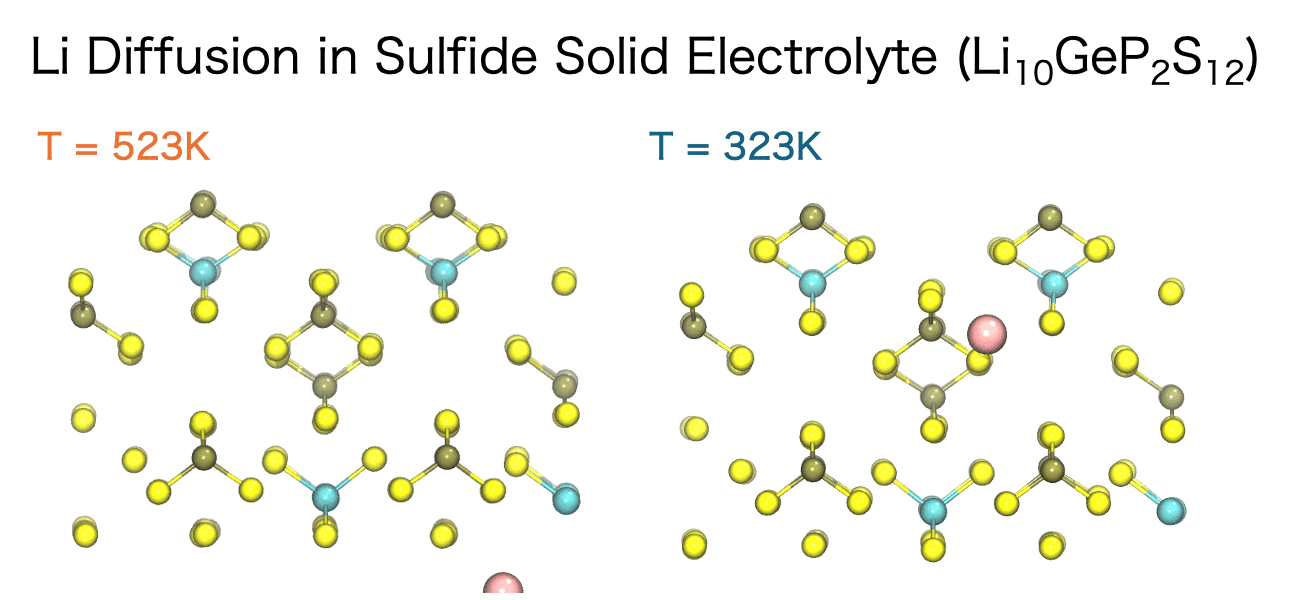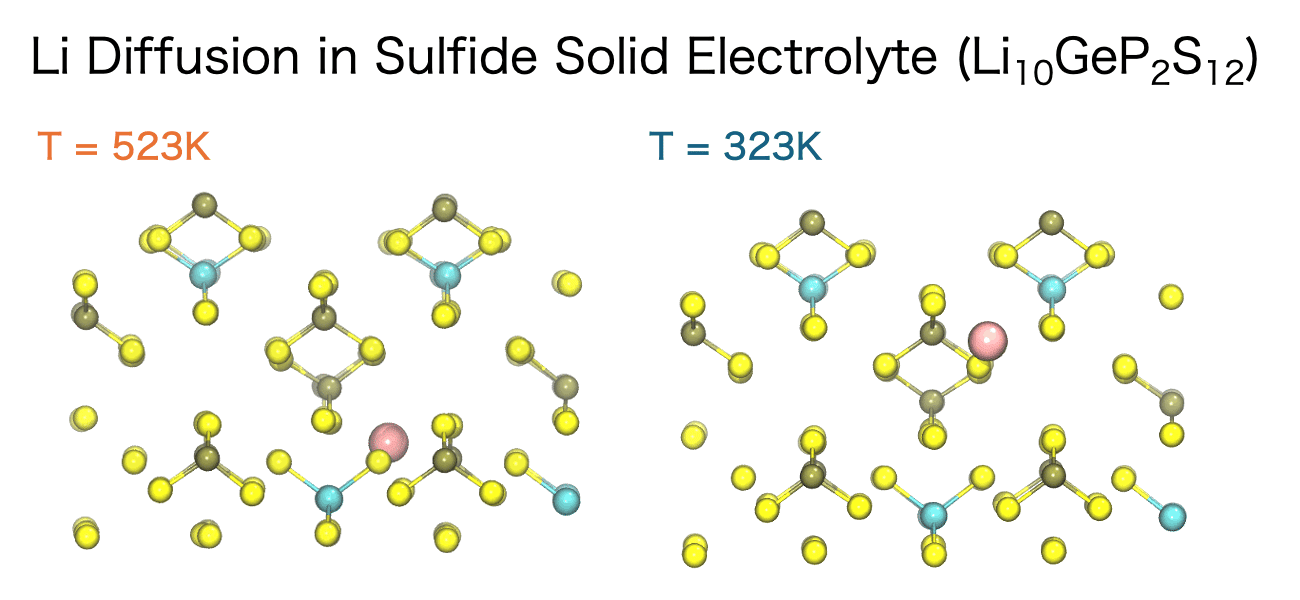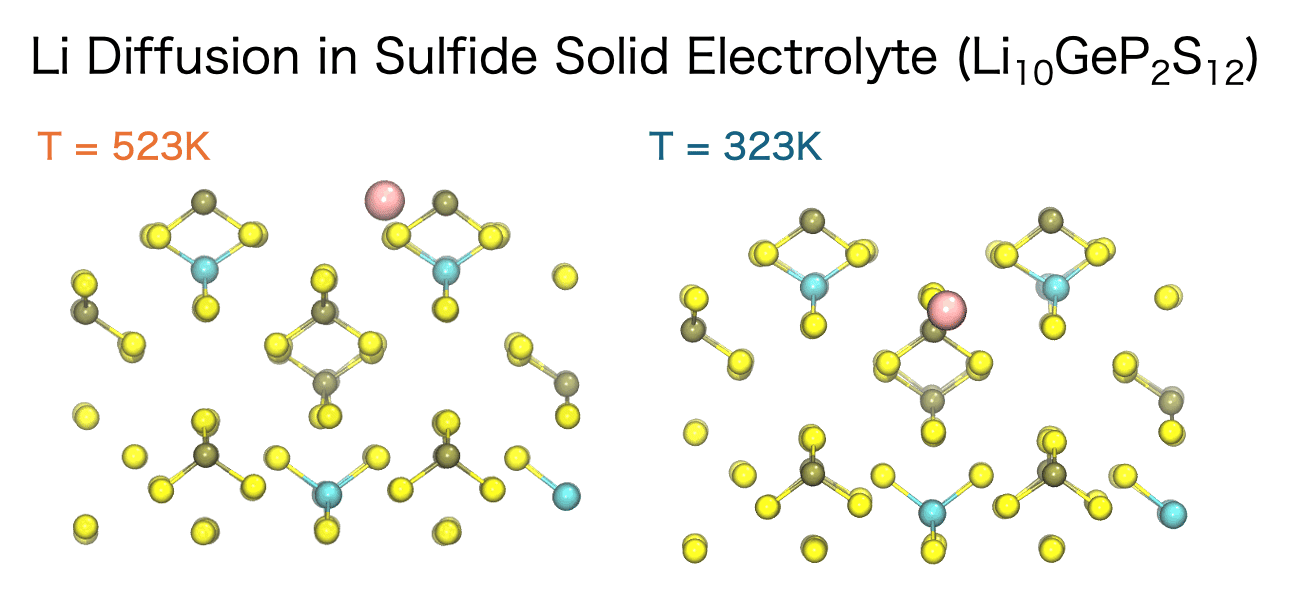
液体中のイオン伝導性、固体電解質中のイオンの移動挙動、高分子中の低分子の拡散など、イオンや分子の拡散は材料の化学的、機械的特性において重要な意味合いを持ちます。そして、分子動力学シミュレーションを用いるとイオンや分子がどのような経路で、どのような速さで移動しているのかを直接観測することができます。
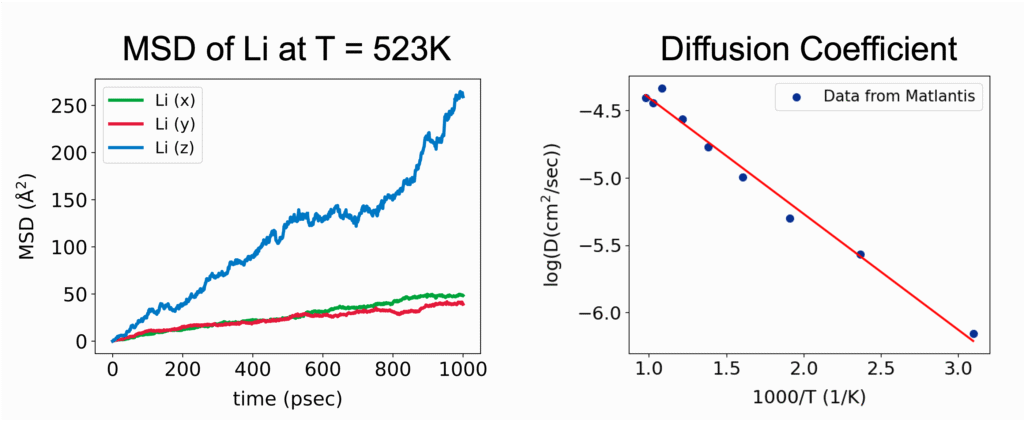
このイオンや分子の移動の速さは、拡散係数 (Diffusion Coefficient)と呼ばれる指標によって定量化することができます。分子動力学シミュレーションでは、平均二乗変位(Mean Square Displacement; MSD)の時間変化から拡散係数を計算することができます。MSDとは、粒子iの初期位置 ri(0)から時間tにおける位置ri(t)までの変位ベクトルの二乗を、全粒子および異なる初期時刻に対して平均した量を指します。
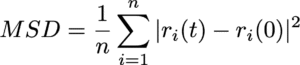
粒子が十分に長い時間経過後に拡散的振る舞いを示す領域においては、MSDは時間に比例して直線的に増加します。この直線的な領域の傾きを用いて、アインシュタインの関係式から拡散係数Dを決定することができます。3次元系における拡散係数は以下の式で定義されます。
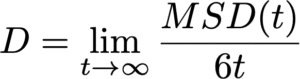
拡散係数の評価によって、シミュレーション結果を実験と整合性を検証しながら、材料内部でのイオン・分子の輸送メカニズムを定量的に理解することができます。さらに、温度や圧力、組成を系統的に調べることで、拡散過程を支配するエネルギーバリアを詳細に検討できるため、材料開発の加速やプロセス条件の最適化に大きく貢献します。
(3) 材料の強さや変形を評価する: 応力-歪み曲線
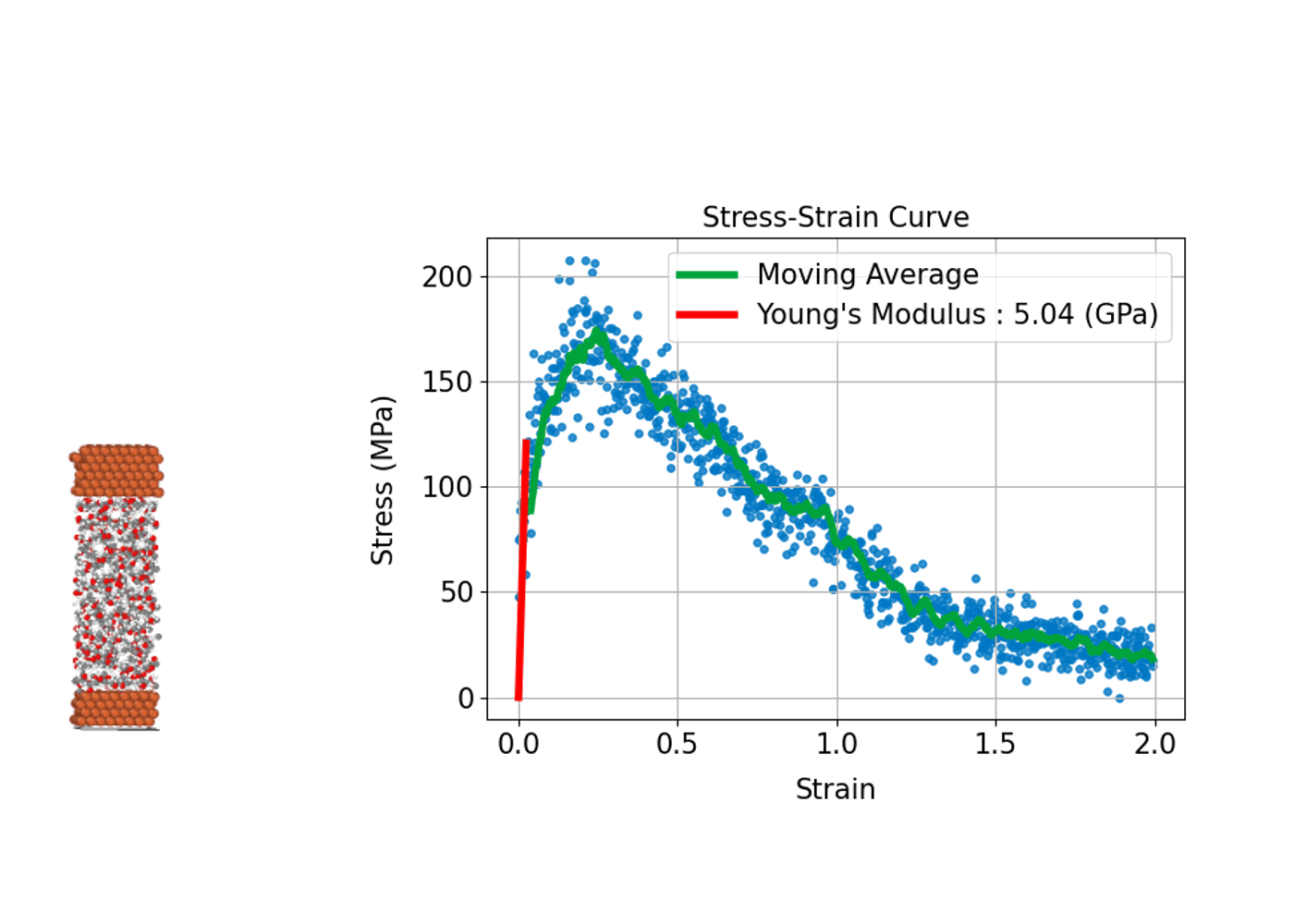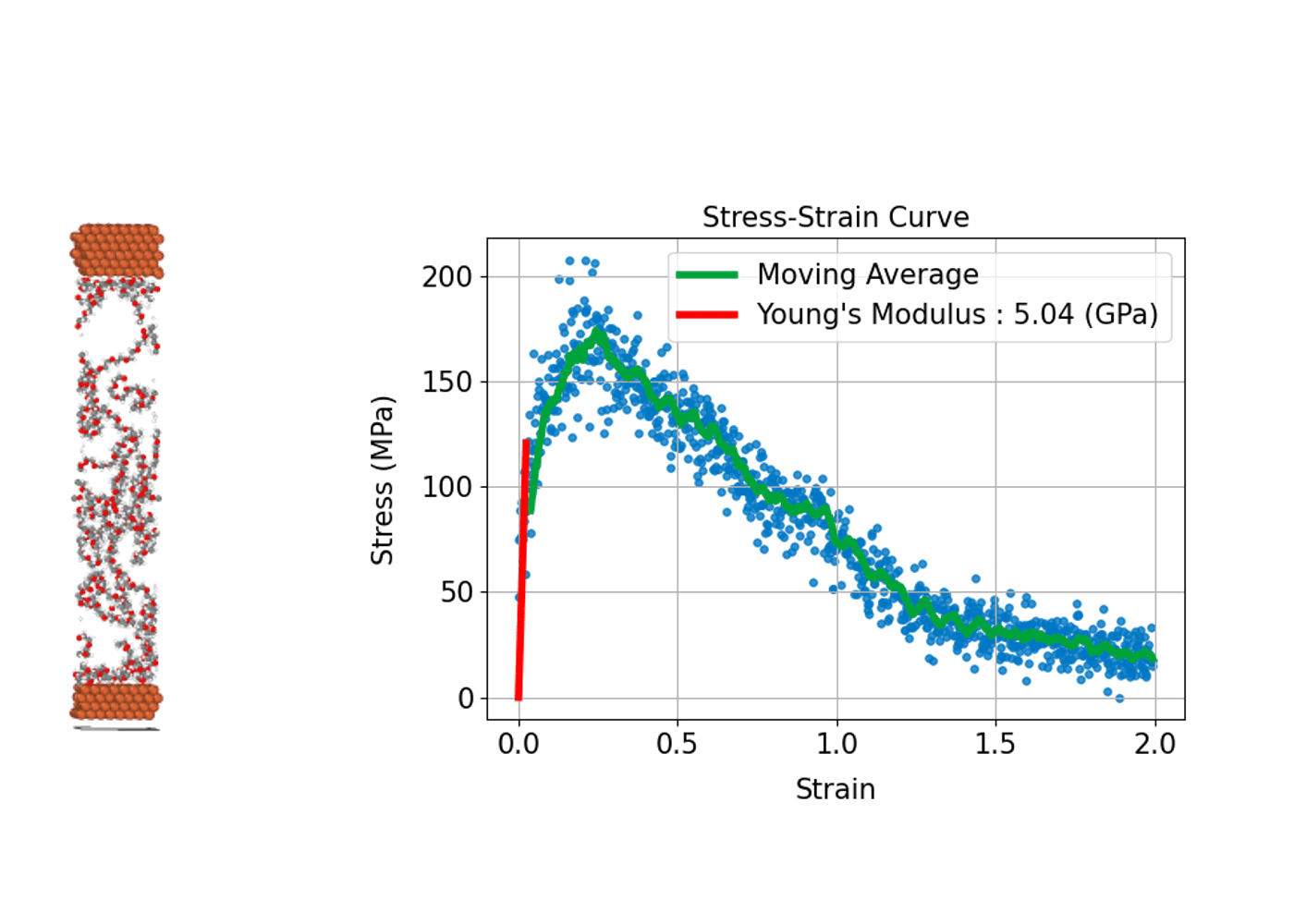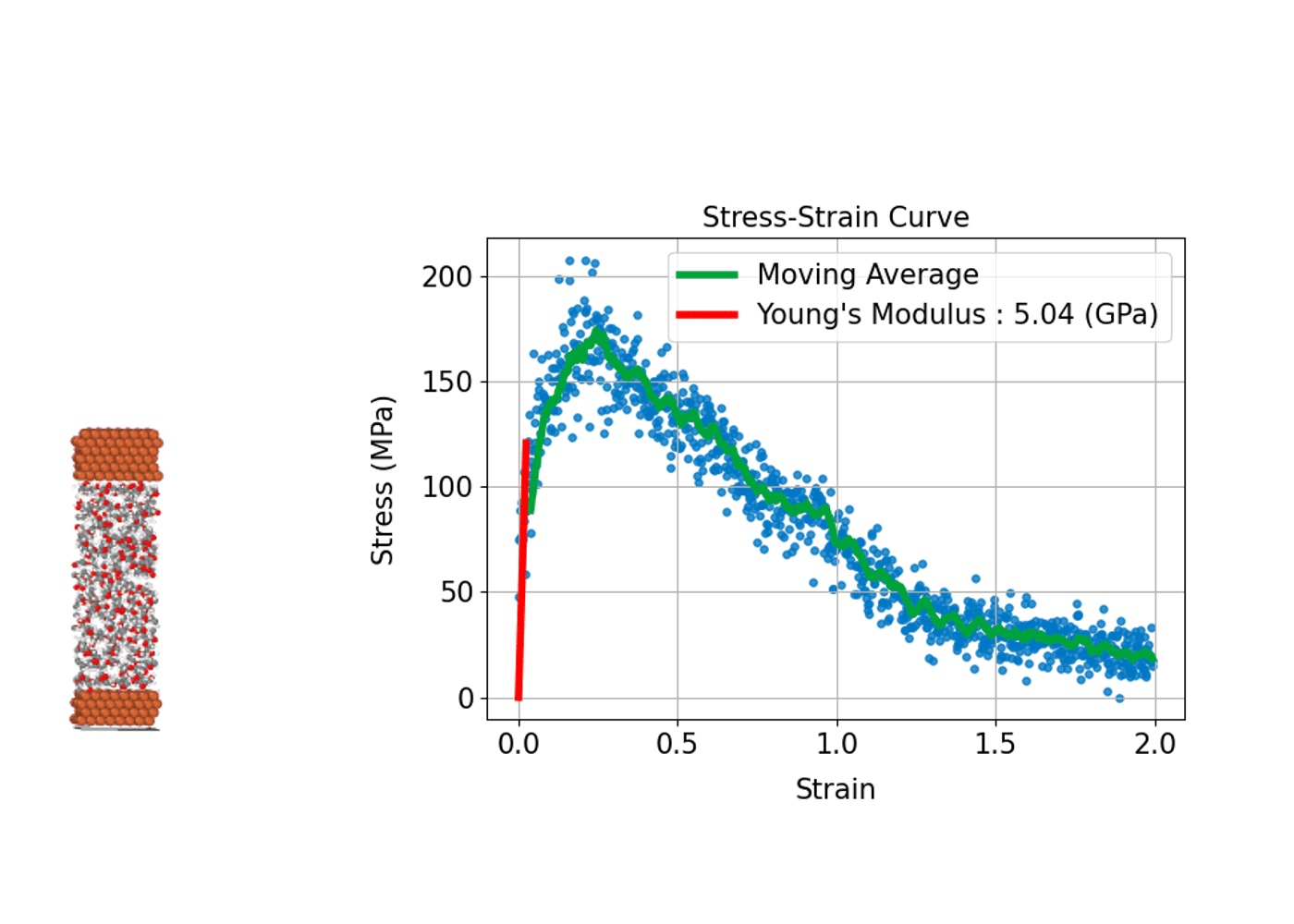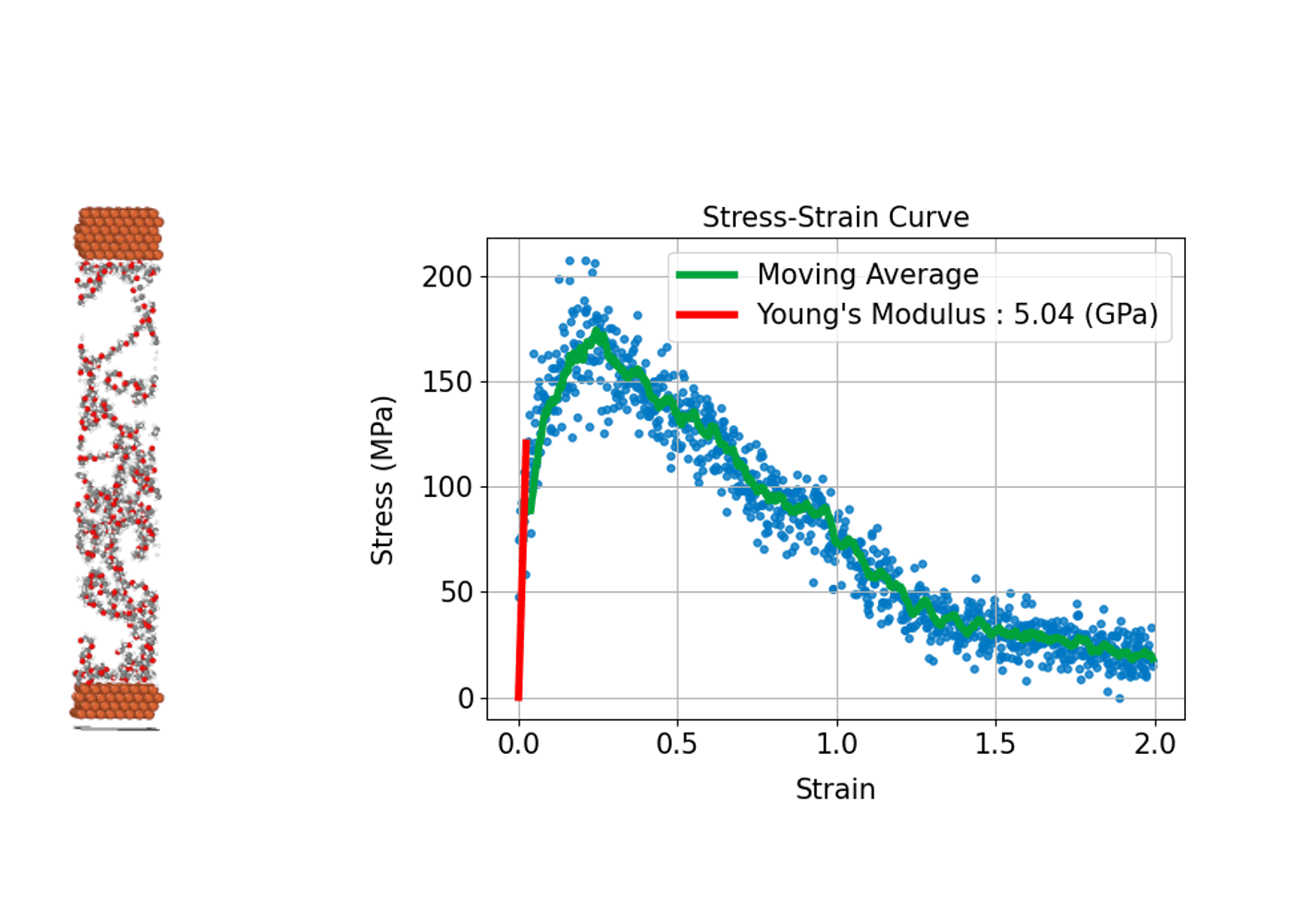
材料が外部応力下でどのように変形し、どれほどの強度を持つかを評価することは、構造材料の設計や開発において重要です。分子動力学シミュレーションは、原子スケールで材料の応力-歪み曲線(Stress-Strain Curve)を導出し、材料の巨視的な機械特性と微視的な変形メカニズムとの関係性を明らかにすることができます。
具体的には、シミュレーションにおいて計算セルに引張り、圧縮、せん断などの変形(歪み)を段階的に与えます。系内に誘起される応力を計算することで、応力-歪み曲線を作成します。この曲線から、ヤング率(弾性領域での応力-歪みの比例係数)、降伏応力(塑性変形が始まる点)、引張強度(材料が耐えることができる最大応力)などの機械的特性を評価することができます。
分子動力学シミュレーションでは材料の塑性変形や破壊プロセスが始まる初期の兆候など微視的プロセスを直接観察できる点が大きな利点です。金属、セラミックス、高分子、ナノ材料など、幅広い材料系の力学的特性の解析への応用が進んでいます
(4) 複雑な動きから本質を抽出する: 主成分解析
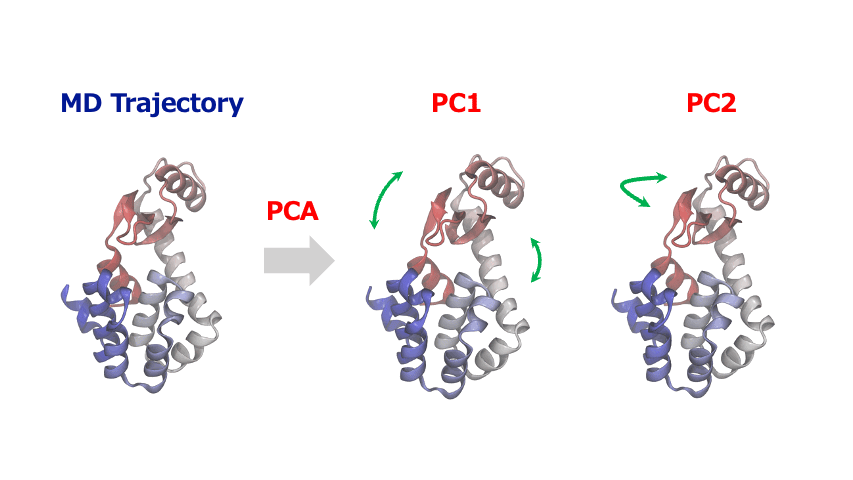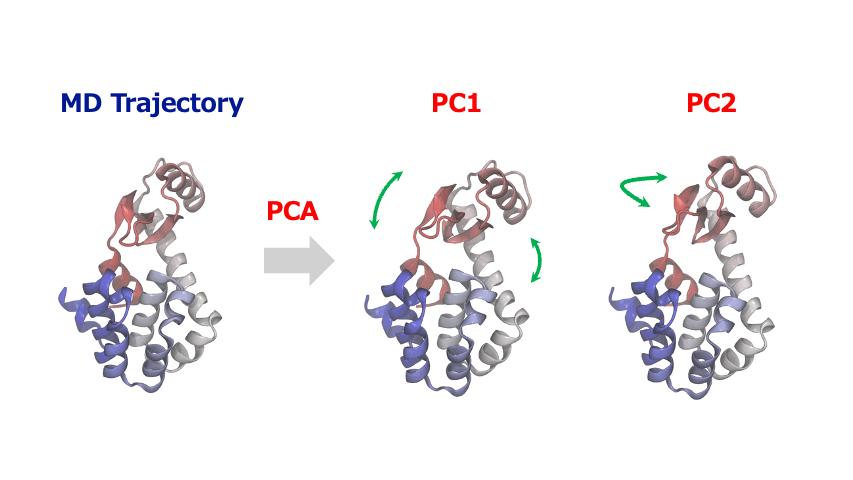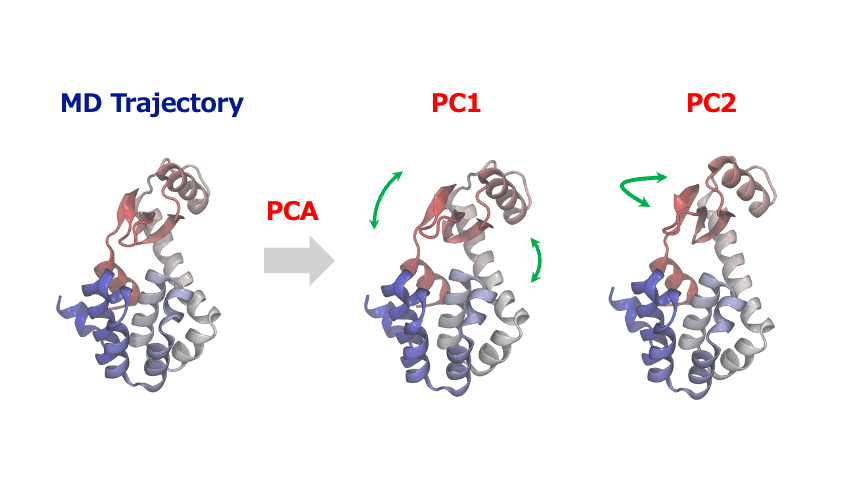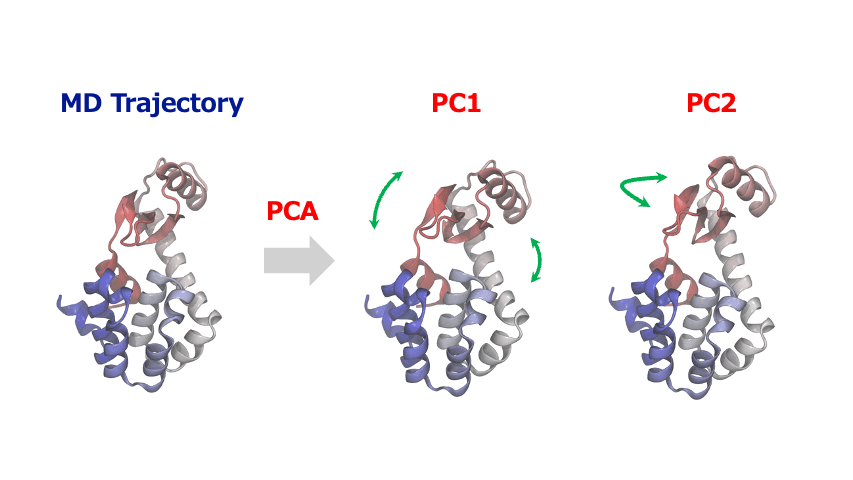
分子動力学シミュレーションから得られる原子座標の時系列データは多くの自由度を含む高次元データであるため、その中から協調的な運動や構造変化の重要なパターンを見出すこが大変なことがあります。このような時、主成分分析 (Principal Component Analysis; PCA)を使えば、原子・分子の複雑な動きから本質的な情報を抽出することができます。
主成分解析は、原子の変位に関する共分散行列または相関行列を対角化することで、分散が最大となる直交基底(主成分)を特定します。一般的に、最初の数個の主成分(PC1, PC2…)が系の大きな構造変化を捉えます。得られた主成分空間へトラジェクトリデータを射影することにより、タンパク質のドメイン運動やアロステリックな構造変化、結晶構造の相転移に伴う協調的な原子変位など、系を特徴づける代表的な運動を明らかにすることができます。
さらに、主成分空間上での構造の分布に対してクラスタリング手法を適用することも有効です。これにより、MDシミュレーション中に観察される準安定状態や中間状態を分類・抽出して、構造的特徴や存在確率(自由エネルギー)などを定量的に評価することが可能となります。
分子動力学シミュレーションの基本的な流れ
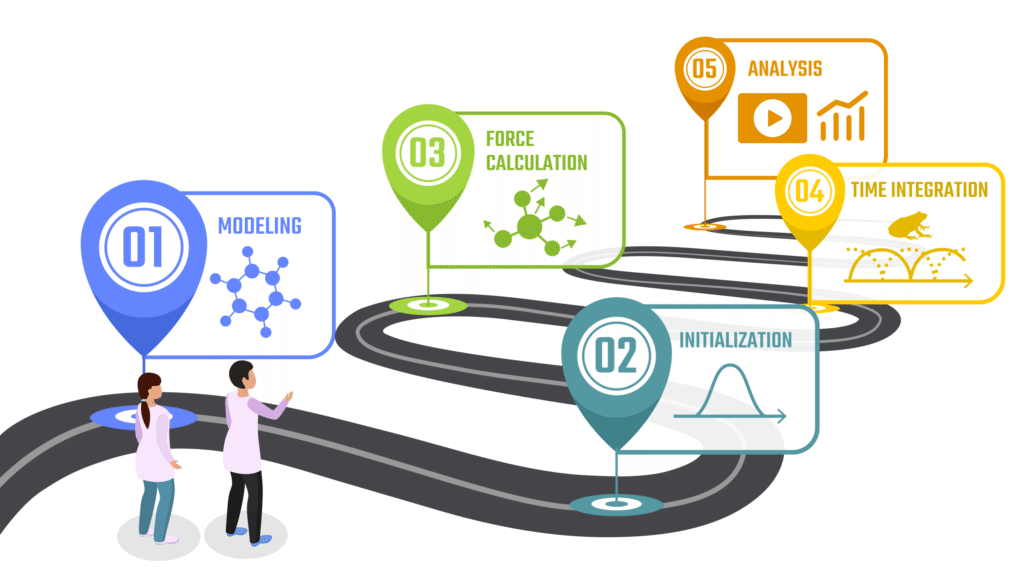
ここまでに見てきたような分子動力学シミュレーションを実行するには、いくつかのステップがあります。この章では、シミュレーションの基本的な流れを紹介します。
(1) 初期構造モデリング
分子動力学(MD)シミュレーションは、まず研究対象となる原子や分子の「初期構造」を準備することから始まります。一般的には既存のデータベースから構造を取得することができます。例えば、材料系のシミュレーションでは、Materials ProjectやAflowなどのオープンデータベースから結晶構造を入手できます。生体分子系ではProtein Data Bank(PDB)に登録されている実験構造、有機分子系ではPubChem、ChEMBLといったデータベースが頻繁に利用されています。
一方、データベースに構造が登録されていても一部の原子が欠損しているなど、そのままシミュレーションのインプットとして使用できないケースも多々あります。このような場合は、モデリングツールを使って欠損部分を適切に補完する必要があります。また、新規材料や未報告の分子系など、既存のデータベースに情報がない場合は、実験データや理論予測に基づいて初期構造をモデリングします。
作成するモデルの精度はシミュレーション結果の信頼性に直結するため、これまでは研究対象に対する知見や豊富なモデリング経験が必要とされてきました。しかし、このような状況は近年大きく変化しつつあります。例えば、2024年にノーベル化学賞を受賞したAlphaFold2をはじめとする構造生成AIの登場により、専門家でなくても分子や材料構造を簡単に予測できるようになってきました。
構造生成AIが生成する構造の妥当性について、現状では依然として専門家の多角的な視点からの判断が不可欠です。例えば、生成される構造が、物理化学的にあり得るものか、既存の類似構造と比較して不自然な点はないか、といった検証は必要です。しかし将来的には、AIが生成した構造を検証して精密化するツールが整備されることで、専門家でなくても高精度な分子や材料構造を直感的かつ容易に準備できるようになることが期待されています。
(2) シミュレーションの初期状態の設定
初期構造が決まると、次に各原子の初期速度を設定します。通常これは、シミュレーションを行いたい温度に応じてマクスウェル–ボルツマン分布に従ってランダムな値を割り当てます。
(3) 原子間ポテンシャルによる力の計算
シミュレーションの中心部となるのが、原子間に働く力の計算です。これは全体のシミュレーション時間の大半を占めるステップであり、高速かつ正確に力を算出するアルゴリズムの工夫が不可欠です。
計算効率を向上させるためには、一定距離以上の相互作用を無視するカットオフ手法や、相互作用領域を複数のCPUに分割して割り当てる空間分割アルゴリズムがよく使われます。計算負荷の高い相互作用計算をGPU上で効率的に計算できるようなアルゴリズムやソフトウェア開発も積極的に行われています。
その中でも特に近年大きな進歩を見せているのが、機械学習 (AI)を活用した原子間相互作用の計算です。機械学習力場は、量子化学計算など高精度な計算から得られる膨大なデータを学習することで、高精度かつ高速に原子間のエネルギーや力を推論します。従来では計算コストの観点から困難だった複雑な材料系に対する高精度な分子シミュレーションが可能になってきています。
(4) 時間積分による運動の追跡
各原子に働く力が計算できれば、それを基にニュートンの運動方程式を数値的に解き、次の時刻における原子位置・速度を求めます。この時間積分を繰り返すことで、原子集団の時間発展、すなわちダイナミクスを追跡することができます。
数値積分には、「ベルレ法(Verlet algorithm)」や「カエル跳び法 (Leap-frog algoright)」がよく使われます。これらのアルゴリズムは、長時間シミュレーションでもエネルギーの保存性や安定性に優れているという特長を持っています (より専門的には、シンプレクティック条件を満たし、影のハミルトニアンが保存されるという性質を持っています)。
また、時間刻み幅(タイムステップ)はシミュレーションの精度と計算効率のバランスを取るために重要です。対象原子の最も速い振動(例えば水素原子の伸縮振動)を正確に捉えるため、一般的には1フェムト秒(10-15秒)程度に設定されます。
(5) トラジェクトリーの解析
分子動力学シミュレーションは、計算を実行して終わりではありません。時間積分を繰り返すことで得られる膨大な原子の座標と速度の時系列データ、すなわち「トラジェクトリ(trajectory)」の中から、意味のある物理的・化学的な情報を引き出す「解析」を行います。このような解析をすることで、シミュレーションと実験結果を比較したり、仮説を定量的に評価することができます。
原子間ポテンシャルの種類と選び方
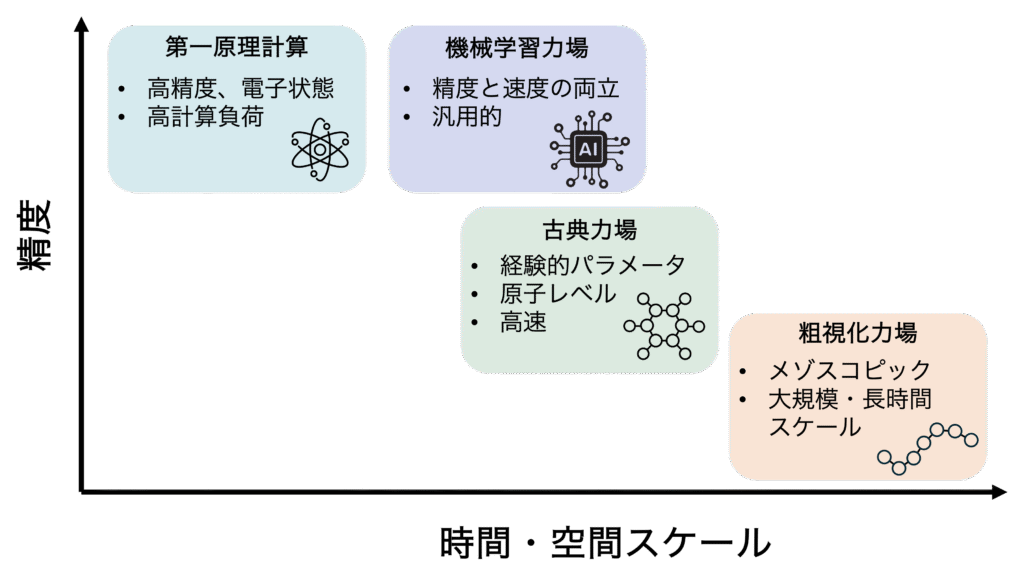
分子動力学シミュレーションの精度、そして扱える現象の範囲を決定づける最も重要な要素の一つが「力場(フォースフィールド)」です。力場とは、原子間の相互作用を記述する数式(ポテンシャル関数)とそのパラメータの集合であり、分子動力学シミュレーションの土台となっています。
研究対象や目的に合致した適切な力場を選択することは、信頼できるシミュレーション結果を得るために不可欠なステップです。本節では、計算化学分野で使われる代表的な原子間ポテンシャルの種類と、それぞれの特長、適用範囲、選び方のポイントについて詳しく説明します。
(1) 第一原理分子動力学: 量子力学に基づく高精度計算
第一原理分子動力学法は、経験的パラメータに依存せず、量子力学に基づいて電子状態を正確に扱いながら原子に働く力を計算して、分子動力学シミュレーションを行う方法です。この方法では、化学結合の形成・切断、原子や分子の表面への化学吸着、触媒反応など、電子状態の変化が重要となる現象を高い精度で再現できることが特徴となっています。
一方で、第一原理分子動力学法は各時間ステップで電子状態を解くための量子化学計算 を繰り返し実行する必要があるため、非常に計算コストの高いシミュレーション手法であることでも有名です。計算機が発達した現在においても、一般的に扱える系のサイズは数百原子程度で、到達できる時間スケールもピコ秒(10⁻¹²秒)程度に限られています。
(2) 古典力場:原子レベルのシミュレーション
古典力場は、あらかじめ定義されたポテンシャル関数と、原子種ごとに最適化されたパラメータを用いて原子間相互作用を記述します。これらの力場パラメータは実験データや高精度な量子化学計算の結果を再現するように調整されており、多種多様な材料や分子系に対して適用することができます。
材料系では以下のような力場(ポテンシャル関数)がよく使用されます:
- Born-Mayer-Huggins (BMH)ポテンシャル: イオン結晶 (アルカリハライド、ケイ酸塩など)
- Buckinghamポテンシャル: 希ガス結晶、分子性固体、酸化物やセラミックス材料
- Stillinger-Weberポテンシャル: 共有結合性の半導体材料(シリコン、ゲルマニウムなど)
- EAM(Embedded Atom Method): 金属および合金系材料
- Tersoff: 共有結合性の強い材料 (シリコン、炭素など)
- Dreiding: 有機分子を中心に、広範囲な元素に対して適用可能な汎用力場
- UFF(Universal Force Field): 有機・無機を問わず広範な元素に適用可能な汎用力場
また、タンパク質、核酸、脂質といった生体高分子の構造と物性を精度良く再現するように調整された、生体分子系に対する力場 (ポテンシャル関数)として
- AMBER (Assisted Model Building with Energy Refinement)
- CHARMM (Chemistry at Harvard Macromolecular Mechanics)
がよく利用されています。
古典力場の特長は計算効率の高さです。GPUを利用すれば数十万から数百万原子規模の系に対しても、マイクロ秒(μs)オーダーの長時間シミュレーションが可能です。
(3) 粗視化力場: メゾスコピックな現象の解析
粗視化モデルでは、複数の原子(例えばアミノ酸残基や高分子のモノマー単位)を一つの粒子として扱うことで、計算コストを大幅に削減します。
この方法を使うことで、高分子材料や脂質膜、ナノ構造体の自己組織化や相分離など、メソスケール領域の現象をシミュレーションで再現可能です。代表的な粗視化モデルとしては
があげられます。
粗視化モデルでは原子レベルの化学構造や相互作用の情報は平均化・単純化されるため、原子スケールの動きや、化学反応などの記述は困難であることには注意が必要です。また、解析したい現象によっては、適切な粒度への粗視化、ポテンシャル関数の設計、パラメータ決定などが必要となるため、実際に使いこなすには技術的な課題が伴います。
(4) 機械学習力場の登場: 精度と速度を両立する革新技術
近年、分子シミュレーション技術において注目されている革新技術の一つが、「機械学習力場」です。これはニューラルネットワークなどのAI技術を活用することで、従来では難しかった精度と速度の両立を実現する画期的なアプローチです。
機械学習力場では、第一原理計算(DFT計算)から得られた膨大なデータ(原子配置に対するエネルギーや、原子に働く力)を「教師データ」としてニューラルネットワークなどのAIモデルに学習させます。その結果、原子間の複雑な相互作用を高精度で再現するポテンシャルを構築することができます。
さらに、元素周期表の幅広い元素をカバーする汎用性の高いニューラルネットワークポテンシャルも開発が進んでいます。その代表例が、弊社が提供する原子レベルシミュレーションプラットフォーム「Matlantis」に搭載されているPFP(Preferred Potential)です。
従来は、新たな材料系で信頼性の高いシミュレーションを行うために、その材料系に特化した力場パラメータの探索・最適化が必要であり、多くの時間と労力がかかっていました。しかし、PFPのような汎用的な機械学習力場を使うことで、材料ごとのパラメータ調整なしに即時的な適用が可能となっています。
また、機械学習力場は第一原理計算並みの精度を維持しながらも、第一原理計算と比較して超高速にシミュレーションできることも特長です。これにより、従来のDFT計算では扱えなかった規模(数万原子)や、長い時間スケール(数十ナノ秒)のシミュレーションが実用的になっています。具体的な応用例としては以下のような複雑系への展開が進んでいます。
- アモルファス材料や高エントロピー合金など、不規則性の高い複雑な構造を持つ材料の物性予測
- 固体電解質中や液体中でのイオンの複雑な拡散経路とダイナミクス
- 触媒表面や溶液中での化学反応機構の網羅的探索
- 合金、セラミックス、有機材料など異種材料が接する界面における材料挙動
機械学習力場の登場により、これまで手が届きにくかった材料系での応用が広がり、分子シミュレーションの可能性はさらに拡大しています。
まとめ
本記事では、原子・分子の挙動をリアルタイムで追跡する「計算上の顕微鏡」である分子動力学(MD)シミュレーションについて、基本的な流れ、原子間ポテンシャル、そして得られたデータの解析方法まで解説しました。従来は第一原理計算、古典的力場、粗視化モデルを用途に応じて使い分けていましたが、最近では機械学習力場の登場により、適用範囲が大幅に拡大しました。
多くの研究者が分子動力学シミュレーションを活用することで、材料研究開発のスピードは、今後ますます加速していくでしょう。分子動力学シミュレーションは、もはや単なる現象解明のツールではありません。実験に先立って新たな材料を合理的に設計することで、材料開発プロセスそのものを変革する強力なツールとなっています。
弊社が提供する原子レベルシミュレータ「Matlantis」は、この変革を加速させるために生まれました。自然界に存在する全ての元素に対応した機械学習力場を搭載しており、アイディアが生まれた瞬間に、多種多様な材料に対してすぐにシミュレーションを実行できる環境を提供します。分子動力学シミュレーションは、まさに次世代の材料開発をリードする中核技術だといえます。
参考文献
[1]「分子シミュレーション –古典系から量子系手法まで–」裳華房、上田 顯 著
[2]「コンピュータ・シミュレーションによる物質科学 分子動力学とモンテカルロ法」共立出版、川添良幸・ 三上益弘・ 大野かおる 著
[3] 「コンピュータ・シミュレーションの基礎(第2版): 分子のミクロな性質を解明するために」化学同人、岡崎進・吉井範行 著