密度汎関数理論(DFT)は、量子力学の原理に基づいて、原子や電子の振る舞いを理解しようとする理論の一つです。DFTの定式に基づく計算(DFT計算)によって、物質の原子レベルでの情報が得られるため、様々な物性計算や現象解明に用いられています。
計算ハード・ソフト両面の発展によるアクセス性の向上や、事例増加に伴う認知の拡大により、材料開発領域においてDFT計算を使った応用計算の報告例が増えている状況です。さらに近年では、マテリアルズ・インフォマティクス(MI)向けに、条件の揃ったデータを生成する目的で利用されるケースもあります。
本記事では初心者を対象として、DFTの理論的な背景、計算可能な現象・物性について解説をします。簡潔さを優先し、厳密さを犠牲にしている部分もありますので、本格的に学習されたい方は専門書[1,2]をご参照ください。
密度汎関数理論(DFT)とは何か
密度汎関数理論(Density Functional Theory: DFT)とは、量子力学の原理に基づいて、原子や電子の振る舞いを理解しようとする理論の一つです。DFTによると、結晶・分子など与えられた構造についての電子密度がわかれば、対応するエネルギーおよび電子状態が一意に決まります。密度汎関数における密度は「電子密度」、汎関数は「関数の関数」を表す専門用語です。電子密度ρは電子位置rから決まる関数ρ(r)であり、DFTに従えばエネルギーEは電子密度ρ(r)で決まるので、エネルギーは電子密度の関数、すなわち汎関数(= E[ρ(r)] )になります。
もし系のエネルギーがわかれば、どのような結晶や分子構造がどのくらい安定なのかを定量的に比較することができます。また電子状態からは、バンドギャップ・分子軌道や原子上の正味電荷など、物性や反応性に関わる重要な情報が得られます。
現在主流となっている計算法では、Kohn-Sham方程式という数式を、入力した構造と計算条件の下、専用プログラム・計算機を使って数値的に計算します(DFT計算)。DFT計算から得られる情報を使って、基礎から応用まで数多くの計算例が報告されています。
計算化学におけるDFTの位置付け
一般的に「計算化学」とは、物理・化学に関する現象を数学的にモデル化し、コンピューター(計算機)上でシミュレーションすることで、理論的な解析や予測を行う領域・手法を指します。特に物質の物性や反応については、原子や電子の状態が支配的であり、そのスケールの領域を理論的に取り扱うためには、量子化学に基づいた計算が必要です。DFTは量子化学をベースとする理論の一つであり、波動関数理論(Schrödinger方程式)と同列に位置付けられます。
Figure1に、DFT計算のターゲットとなる空間・時間領域を示します。現実的にDFT計算が対応できる領域はnm・nsのオーダーであり、これを超えるサイズ系への適用は実質的に不可能です。したがって、より大きい・長い時間での物性や現象を見たい場合には、スケールに応じた別の計算方法を用いる必要があります。
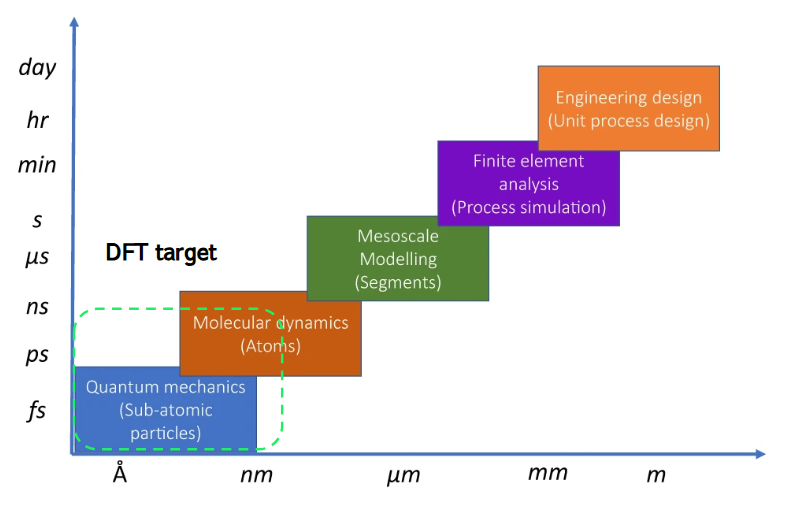
Figure1. 計算化学が取り扱う空間・時間スケール領域とDFT計算のターゲット領域(文献[3]のFig.1から引用・一部改変。Licensed under CC BY 4.0).
DFT計算はどのような分野に使われているのか
DFT計算は、電子・原子が関わる種々の物性計算に有効であり、さらに計算ハード・ソフトの発展もあって、応用計算例の報告が年々増加している状況です。マテリアル分野に関する論文(2010-2023年・約10万件)ついて、内容に関するクラスター解析を行い、可視化した結果をFigure2に示します。DFTの近くには、電池、触媒、水素貯蔵材料、光学材料など、持続可能社会の実現にとって重要な技術が配置されています。この2Dマップは、これらの領域の研究開発において、DFT計算が広く活用されていることを示唆しています。
DFT計算が使用されている論文数は現在も増加傾向にあり、今後も最先端材料の開発に重要な役割を果たすと考えられます。DFT計算が使われている特許も出願もされており、企業の開発スピードや競争力に大きく影響する、重要な要素技術と言えます(詳細は当社HP内にて公開している調査レポートをご参照ください)。
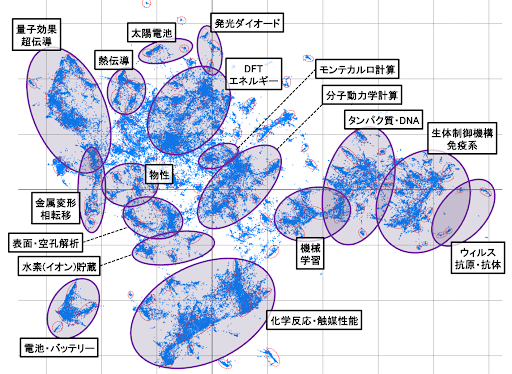
Figure2. マテリアル分野における学術論文約10万件に対するクラスター解析の2Dマップ.
DFTで計算可能な物性・現象
冒頭で説明したように、DFT計算では系のエネルギーと電子状態が得られます。この基本的な情報を利用して、様々な物性や現象の計算が実施できます。
DFT計算では、対象とする物質系によって、計算方法や計算できる物性が異なります。ここでは大まかな系の分類として、「固体・周期系」と「分子系」を考えます。「固体・周期系」とは、金属や半導体などの固体や表面、アモルファスや溶液などの凝集構造を指します。入力構造が周期的に並んだ構造を想定することで(周期境界条件)、無限に大きな系に対する計算が可能です。原子・分子の集合体としての電子状態や物性を計算したい場合には、固体・周期系向けの計算方法を用います。
「分子系」とは、文字通り水(H₂O)やメタン(CH₄)などの分子や、それらが相互作用したクラスターなどを指します。通常真空中での計算になりますが、溶媒効果を加味した計算も可能です。分子単体での性質や、均一系の反応を高精度に計算したい場合などには、分子系向けの計算方法が適しています。
以下ではDFT計算で算出できる、物性・現象の一部をご紹介します。
構造特性
DFTでは、入力した構造に対するエネルギーだけでなく、原子に働く力を計算できます。この力がゼロになるように構造変化させる計算によって、現実に対応する安定構造を求めることができます(構造最適化)。電子状態や静的物性については、構造最適化後の構造を使って議論することが一般的です。構造最適化は0 Kの条件で計算される点はご注意ください。
結晶のように周期的な構造については、繰り返し単位となるセルを設定し、周期境界条件を適用して計算します。この場合、原子位置だけでなく、格子定数も構造変化の対象として最適化できます。計算から得られた安定構造は、実験から得られる構造、例えばX線構造回折等の分光学的データと直接比較が可能です。
また、構造に関連する物性の計算例としては、弾性定数が挙げられます。原子のわずかな変位に対するエネルギー変化を計算することで、ヤング率、体積弾性率、せん断弾性率などを求めることができます。これらの弾性定数は、構造材料や機械部品などで重要になる物性値であり、ミクロな系の計算からマクロな物性値が得られる一例です。
バンド構造・分子軌道
DFTでは、物質中の電子状態に対応する、バンド構造や分子軌道を得ることができます。固体・周期系であれば、伝導帯と価電子帯のエネルギーから、バンドギャップが計算できます。バンドギャップは電導性や光学特性に直接関連するため、半導体などの材料開発にとって不可欠な情報です。
分子においては、分子軌道のエネルギー準位や空間的な分布が計算できます。特に、最高被占軌道(HOMO)や最低非占軌道(LUMO)のエネルギー準位は、化学反応、光吸収や電子輸送特性に関連しています。これらの情報は、例えばポリマー材料の安定性を議論したい場面などで、非常に有益な示唆を与えてくれます。
またDFTでは、これら軌道に関する情報を変換して、原子上の正味電荷を算出することも可能です。系内の電荷分布を基に、極性や反応性を議論することができます。
熱物性・輸送物性
固体・周期系については、格子振動(フォノン)の分散関係を計算することで、比熱、熱膨張率、熱伝導率などが算出できます。また同様の方法で、自由エネルギー等の熱力学量を計算することも可能です。これらの物性は、熱に対する構造変化の指標として、電子デバイス向けの材料特性評価に使用できます。
分子系についても、分子振動解析の計算が可能です(結果をIRスペクトルとして可視化することも可能)。振動数から分配関数を作ることで、エントロピーや比熱、自由エネルギーなどの熱力学量を算出できます。これによって、有限温度の効果を取り入れた熱力学的な安定性の評価が可能になります。
輸送物性として、拡散係数や粘度も計算可能です。これらは、有限温度での原子の時間発展を追跡する手法(分子動力学法: MD)を用いて計算できます(MDに関するブログ記事もご参照ください)。特に拡散係数は、固体電解質やプロトン伝導膜など、電池関連材料のイオン伝導性評価によく用いられています。
応答物性
DFT計算では、外場(電場、磁場、光など)に対するエネルギー変化を計算することで、それぞれの応答物性を得ることができます。
外部電場に対する応答として、分極率、誘電率、誘電損失などが計算可能です。これらは、コンデンサやセンサー向けの材料設計に重要な物性です。また外部磁場に対する応答からは、構造の磁気モーメントや磁化率、NMRスペクトルの化学シフトなどを計算することができます。これらの物性は、永久磁石や磁気記録媒体向けの材料評価に利用されます。
また、物質の光に対する応答については、時間依存DFT(TD-DFT)によって電子励起状態のエネルギーや遷移確率が計算できます。これらの情報から、UV-Vis吸収・発光スペクトルをシミュレートすることが可能です。一重項および三重項励起状態のエネルギー差も計算できるため、熱遅延蛍光材料向けの発光分子の探索に応用されていたりします。
化学反応
DFTでは、反応物・中間体・生成物などの安定構造だけでなく、実験的に解析の難しい遷移状態構造の計算ができます。得られた構造のエネルギー差から、対応する化学反応の反応エネルギーや活性化エネルギーを算出することが可能です。これらの情報を基に、反応経路に沿ったエネルギープロファイルを作成することで、反応の律速段階や選択性などを定量的に議論できます。
化学反応の解析は、DFT計算が最も広く利用されている領域の一つです。特に触媒反応は、通常複雑な素反応の組み合わせを数多く含んでいるため、計算による反応経路の解析が非常に有効な手段となります。
触媒の構造や組成を変更して、同様のエネルギープロファイルを作成・解析することで、反応機構解析にとどまらない、触媒反応の合理的な設計が可能になります。触媒の均一・不均一を問わず、DFT計算は様々な触媒開発に応用されています。
DFT計算の課題と対応
DFT計算は、前節で述べたように、時間・空間的に人間の眼では追えない構造・現象の理解および物性計算に大きな力を発揮します。
DFT計算のもう一つのメリットは、計算機を仮想実験スペースとして、思いついた構造や条件等のアイディアをすぐに試すことができる点です。仮想実験であるため、試薬を購入するコストもかからないし、安全で管理や後片付けも不要です(ファイル・フォルダの整理は必要ですが)。もし計算が実験よりも早く実施できる状況であれば、実験前の理論的な材料スクリーニングなども可能になります。
このように、DFT計算は様々な利点を持つ強力な手法ですが、その一方で原理的・実用的な課題も存在します。ここでは、DFT計算の課題とその対応について簡単にまとめます。
計算精度と汎関数
DFTなどの計算化学的な手法の理想形は、実験と一致する結果を与えることです。室温で平衡状態にある系 A ⇌ B においては、わずか1.3 kcal mol¯¹のエネルギー差で、それぞれの存在比が10倍異なってきます。このような差を計算で議論するためには、小数点一桁 kcal mol¯¹レベルの精度が必要です(化学的精度)。
DFT計算は、解の存在が理論的に保証されている一方で、解くべき式(汎関数)の形が正確に分かっていないという実用上の課題を抱えています。この式の組み立て方に任意性があるため、多種多様な汎関数が提案されており、計算精度は使用する汎関数に依存します。精度の高い汎関数は、一般的に相互作用を表現する項を付け加えるような形で構築されるため、計算量・計算時間は増加してしまいます。このように、DFT計算を行う際は、用途や精度・計算コストを考慮して、汎関数を選択する必要があります。
現状、どのような系に対しても化学的精度を達成するような、普遍的な汎関数は報告されていません。ただ、相対値であれば実験との相関が取れる場合も多く、限界を理解しつつ適切な汎関数を用いて計算を実行することが、現実的な落とし所となっています。DFTの汎関数については、現在も最先端レベルで研究が続けられており、より精度の高い汎関数の開発が進んでいる状況です。
計算時間とサイズ
DFT計算は入力として原子の三次元座標を利用しますが、その値をKohn-Sham方程式に代入するだけでエネルギーや電子状態が求まる、という単純な形式になっていません。実際は電子状態に関する変数をパラメータとする繰り返し計算を行い、収束した値を解とします。
この繰り返し計算の性質に加え、一般的なDFTでは、系の電子数の3乗に比例して計算時間が増加します。計算の種類にもよりますが、原子数が多くなると、一つの計算に数週間から数カ月の時間がかかる場合もあります。現実的な時間内で計算可能な系のサイズとして、100-200原子程度がDFT計算で扱える限界となっています。
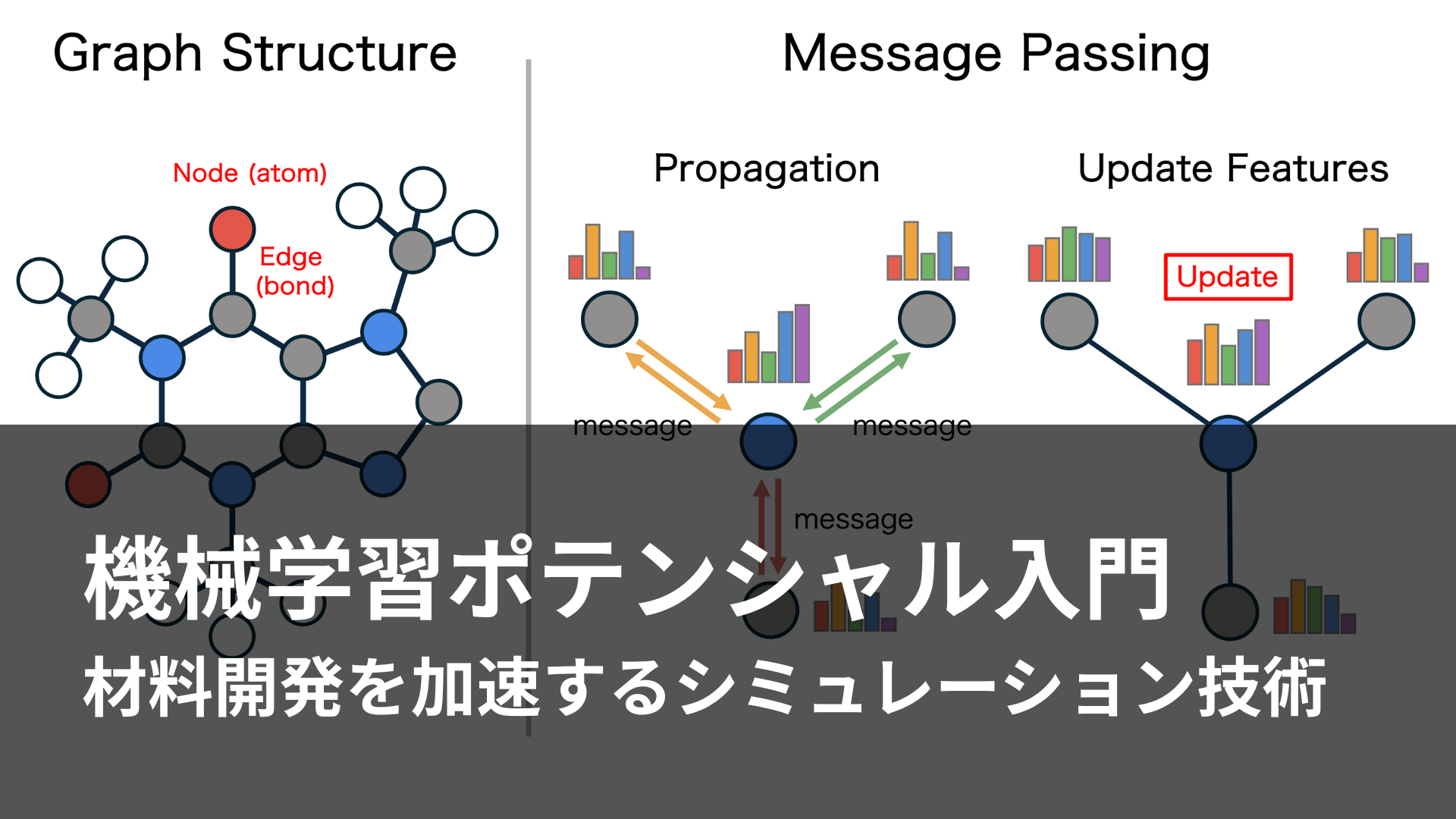
これらの課題に対し、機械学習の技術を応用してDFT計算を加速させる取り組みが、産・学両面から盛んになされています。その一つが、DFT計算の結果を再現する機械学習モデルを作成する事です(機械学習ポテンシャル)。この手法を用いると、DFT相当の精度で超高速に系の計算ができるようになります。当社製品のMatlantis内で使用可能なPFPも、機械学習ポテンシャルにあたります。機械学習ポテンシャルによって、DFTそのものでは計算時間的に不可能なサイズ系の計算や、ハイスループット計算への応用が可能になります。
まとめ
本記事では、密度汎関数(DFT)とは何でどんな計算ができるのか、どのような利点・課題があるか、についてご紹介しました。研究開発の効率化が求められる中、DFT計算を利用した材料開発は、今後ますます広がっていくと考えられます。DFTは、精度・速度の両面で最先端レベルの改良が進められており、さらにAI技術との組み合わせによって、大きなブレークスルーが起きる可能性も期待されます。
本記事が、初心者にとってDFT計算・計算化学を理解する一助となれば幸いです。次回の応用編では、DFTを使った応用計算の報告について、論文や特許を例に挙げてご紹介する予定です。今すぐにお手元の環境で計算を試してみたいという方は、当社のブログ記事やAtomistic Simulation Tutorialもあわせてご参照ください。
参照リンク
- R・G・パール、W・ヤング著、狩野 覚・関 元・吉田元二監訳 (1989).『原子・分子の密度汎関数法』(シュプリンガー・ジャパン).
- 常田貴夫 (2012). 『密度汎関数法の基礎』(講談社).
- Choudhary, K., Garrity, K.F., Reid, A.C.E. et al. npj Comput Mater 6, 173 (2020).