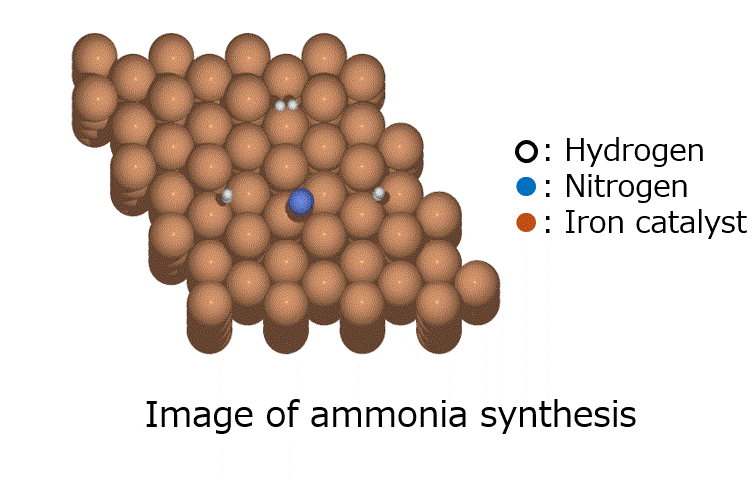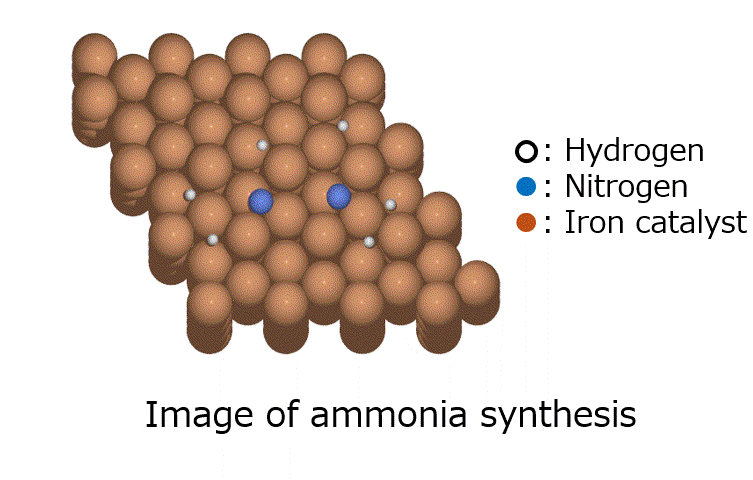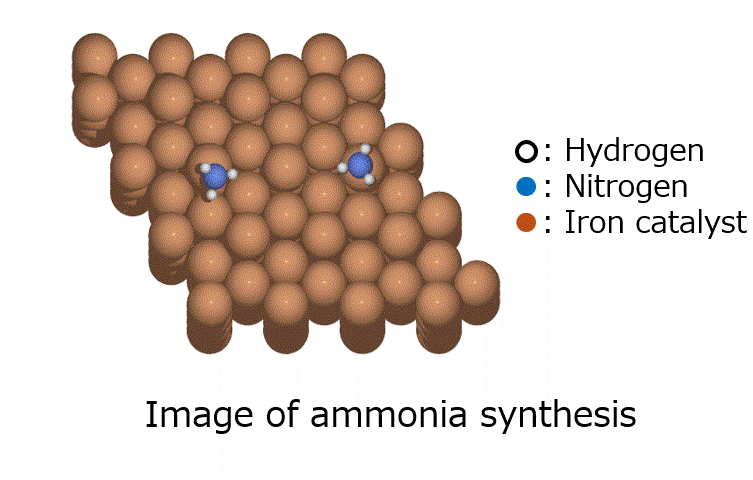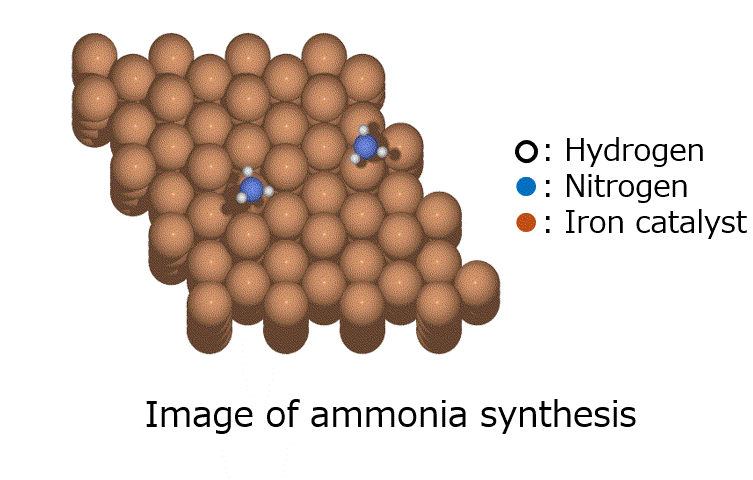
テーマ概要
弾性定数テンソルは、材料の弾性挙動を特徴付ける重要な量である。弾性定数テンソルの成分が分かれば、種々の機械的特性を計算できる。実用上重要な量の1つとして、材料の弾性変形に対する抵抗力を示す弾性率がある。例えば、高い機械的応力を受ける人工構造物には、通常数十から数百GPaの大きな弾性率を持つ材料が必要である。一方、生体適合用途の材料は高分子であることが多く、数MPaから数百MPaの弾性率を示す。
分子性結晶は、硬い材料と柔らかい材料の中間程度のヤング率を示し、光電子材料、アクチュエータ、および、医薬品の製剤において重要である。しかし、大きなサイズの結晶の作製が困難であること、および、対称性が低いために多くの成分を測定する必要があることから、弾性定数テンソルの測定はあまり行われてこなかった。
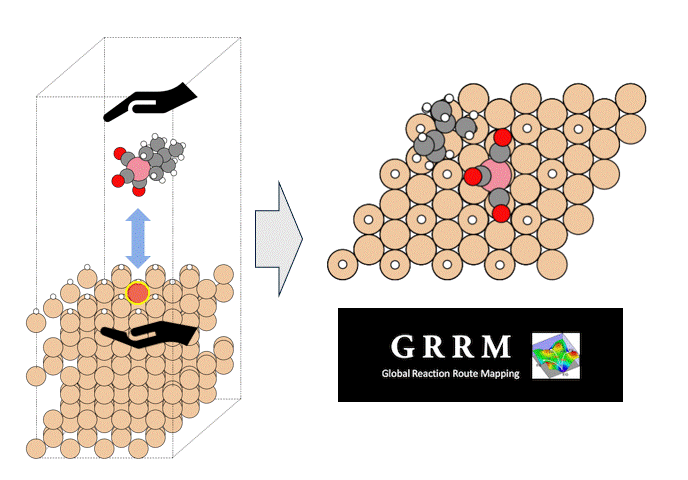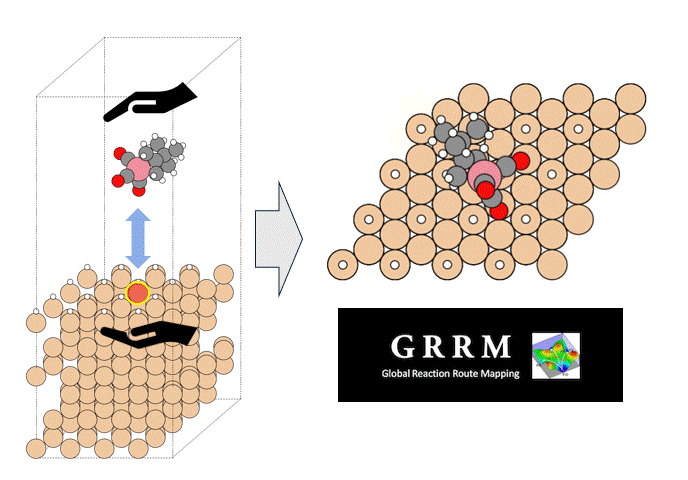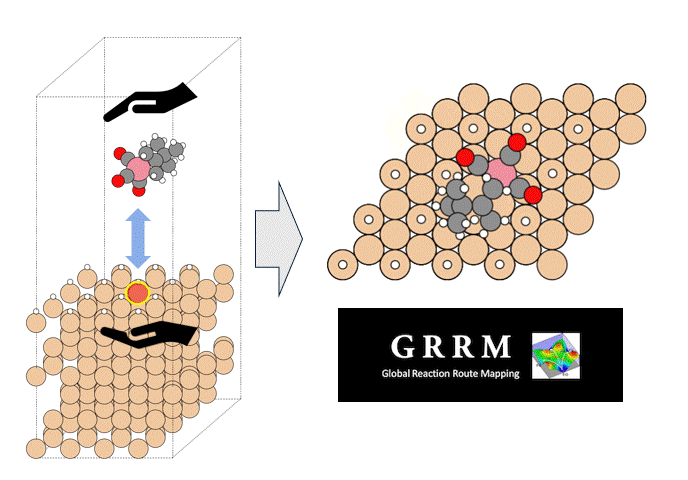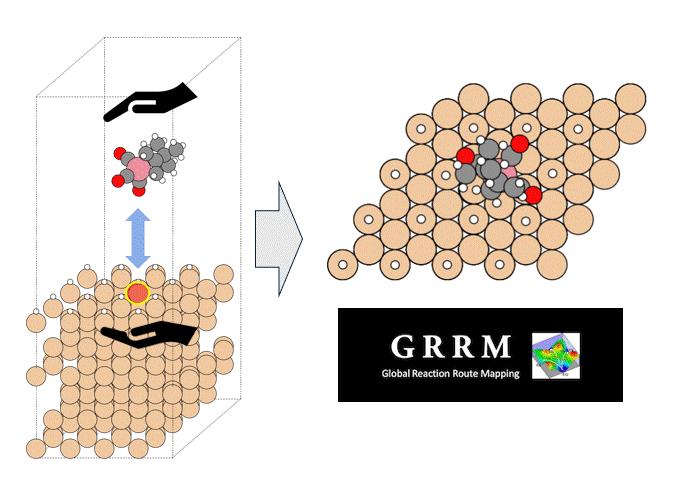
そのため、実用的な分子結晶の開発には、計算による材料スクリーニングが有効である。従来、弾性テンソルの計算には理論計算(DFT、HF)が用いられてきたが、計算負荷が膨大であった。近年発展したニューラルネットワークポテンシャル(NNP)は計算負荷が低いものの、無機材料などへの適用事例が多く、分子性結晶への有効性はわかっていない。
この研究では、分子結晶の弾性定数計算についてNNPの有効性を検証した[1]。
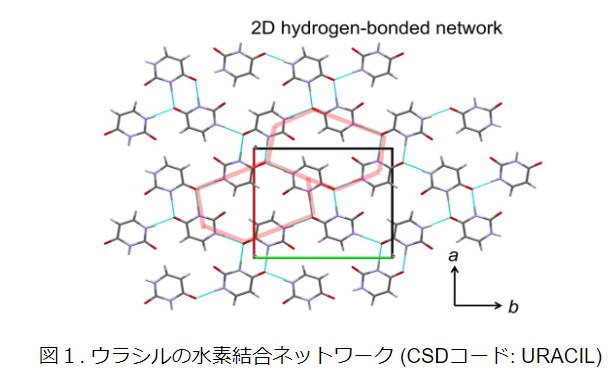
計算モデルと計算方法
最初に、NNPのベンチマークを行った。ベンチマークには文献 [2]にある以下のデータを用いた:80種の化合物に対する123の弾性テンソルの実験値、44種の化合物に対するHartree–Fock法(S-HF-3c)の計算値、および、11種の化合物に対するDFT-Dの計算値。S-HF-3cのデータにある化合物について、PFP (v4.0.0), CHGNet (v0.2.0)[3] を用いて体積、および、弾性テンソルを計算した。その結果、PFPの精度はHFやCHGNetよりも高く、DFTの結果と同程度であった。
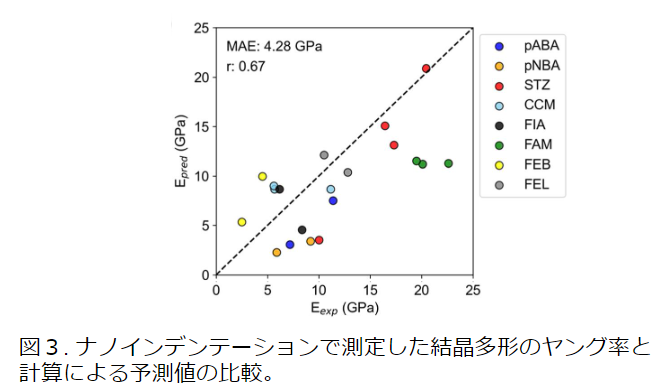
分子性結晶には、配列の異なる結晶多形が存在することが多く、結晶構造の違いが弾性定数に影響する。NNPが結晶多形による弾性定数の違いを表現できれば、実験と比較する上で有用である。そこで、8つの化合物の結晶多形についてナノインデンテーションから求めたヤング率の実験値[4]について、PFPによる計算を行い比較した。
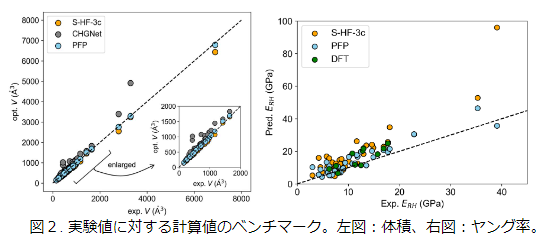
計算結果と展望
ヤング率の計算値は実験におけるおおよその傾向を再現した。4つの材料(pABA, pNBA, STZ, and FEB)について実験における結晶多形の傾向を再現した。一方、他の材料については多形の違いを表現できない(FAM、CCM)、もしくは、実験と逆の傾向 (FIA, FEL)を示した。ただし、ナノインデンテーションの実験についても、真の値に対して測定条件に依存した誤差が含まれる。構造とヤング率の関係に着目すると、分子性結晶の弾性特性は分子間の水素結合に依存することが知られている。PFPの計算値は実験値と完全には一致しなかったものの、結晶構造中の水素結合とヤング率の傾向を再現しており、NNPは弾性定数の予測に有効であると考えられる。
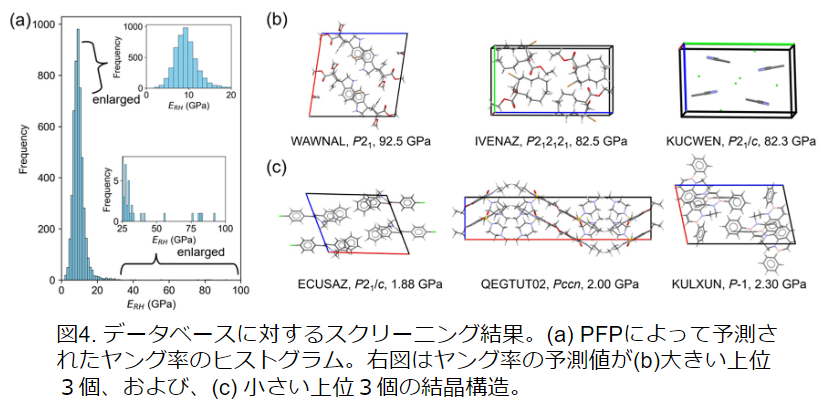
また、NNPを用いて低ヤング率、および、高ヤング率の分子結晶についてスクリーニングを行った。Cambridge Structure Database (CSD)からランダムに5,000個の結晶構造を選び、ヤング率を計算した。その結果、従来知られているものよりもヤング率の高い分子結晶が得られた。この結果は、PFPが有機結晶の材料探索に有用であることを示す。
計算条件

参考文献
[1] T. Taniguchi, CrystEngComm, 2024, 26, 631 [2] P. R. Spackman et al., Angew. Chem., 2022, 61, e202110716. [3] CHGNet. https://chgnet.lbl.gov/ [4] B. P. Gabriele et al., CrystEngComm, 2021, 23, 2027–2033.事例提供者プロフィール
早稲田大学 データ科学センター

タグ
本事例の公開日:2024.04.25