はじめに#

「拡散」とは、ブラウン運動によって引き起こされる原子や分子の変位のことです。
原子や分子の拡散の度合いを表す量として、拡散係数があります。
シミュレーション上では、MDトラジェクトリの平均二乗変位から拡散係数を計算します。
PostMDDiffusionFeature
を用いることで、平衡MDのトラジェクトリから自己拡散係数を求めることができます。

計算手法#

平均二乗変位(mean squared displacement, MSD)は以下のように定義されます。

[MSD(t) = frac {1}{N} sum_{i=1}^{N} left ( vec {r_i}(t) – vec {r_i}(0) right )^2]

(N) は粒子数を、 (vec {r_i}(t)) は (i) 番目の粒子の時刻 (t) での位置を表します。

拡散係数とMSDの関係は以下のようになります。

[MSD(t) = 2nDt]

(D) は拡散係数、 (n) は系の次元を表します。
MDシミュレーションの時間の長さが十分であれば、時間とMSDは線形の関係になります。
(D) は 時間 – MSD 曲線を線形フィッティングし傾きを求めることで得ることができます。
また、拡散係数の標準偏差についても、線形フィッティング時の傾きの分散から評価できます。

PostMDDiffusionFeature では、MDのトラジェクトリからMSDを求める手法が2種類提供されています。

例えば、MDトラジェクトリの (0, Delta t, 2 Delta t, … N Delta t) におけるスナップショットがある場合を考えます。
normal法 (method='normal') を指定した場合、 (MSD(2 Delta t)) は0番目と2番目のスナップショットの間の変位 (vec{r}(2Delta t)-vec{r}(0)) から計算されます。
一方、 segment法 (method='segment') を指定した場合、 (MSD(2 Delta t)) は
(vec{r}(2Delta t)-vec{r}(0), vec{r}(3Delta t)-vec{r}(Delta t), …, vec{r}(NDelta t)-vec{r}((N-2)Delta t))
の平均から計算されます。[1]

平均をとっているためsegment法のほうがnormal法よりも精度は良いですが、計算コストが高くなります。
液体の水についてMDを15ps行った際の、H原子とO原子のMSDを以下にプロットします。
segment法で得られた曲線のほうが、normal法よりも変動が少ないことがわかります。

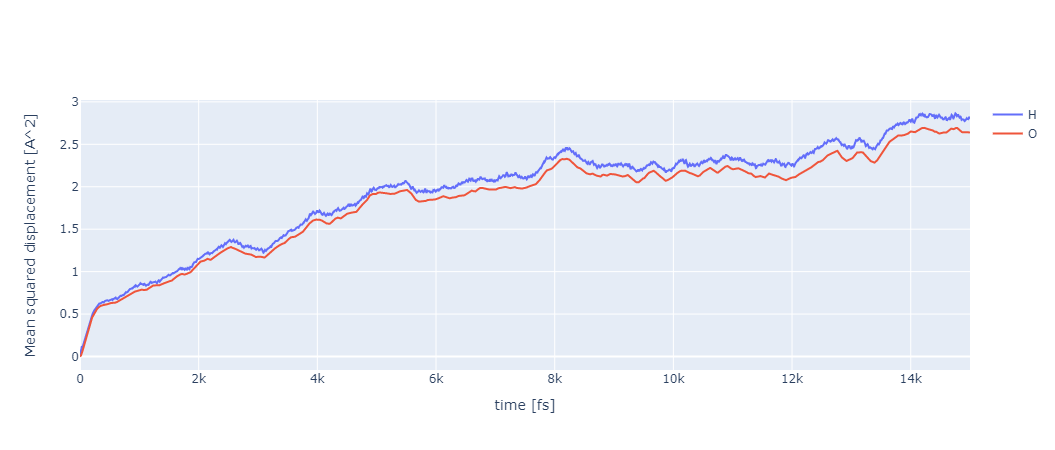
../_images/normal.png

normal法によって計算された平均二乗変位#

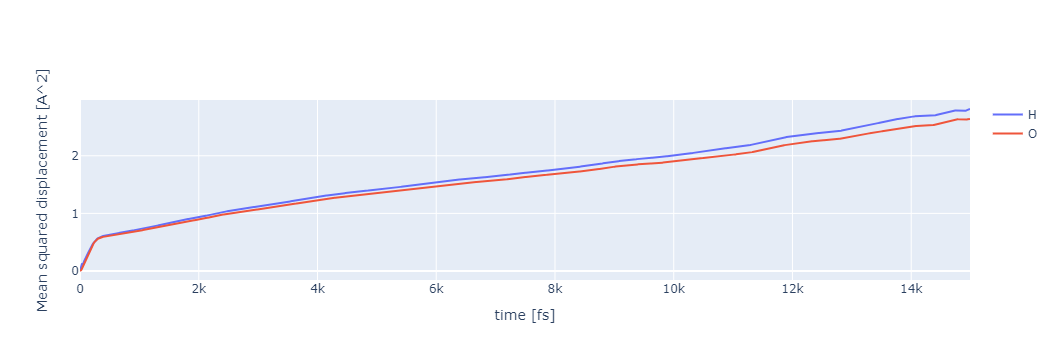
../_images/segment.png

segment法によって計算された平均二乗変位#

注意点として、segment法では、 (t) がMD全体の時間の長さに近くなると、(MSD(t)) を計算するためのサンプル数が少なります。
これは、上図のようにMSD曲線の後半に揺らぎを生じさせることがあります。
大きな揺らぎが現れた場合、線形フィッティングの信頼性に影響が出ることがあります。
また、上図では最初の数百fsでMSDが急激に増加しています。
これは、MSDの最初の部分では原子の長距離拡散よりも局所平衡点付近での原子振動の寄与が大きいことが原因です。
そのため、拡散係数の計算では、MSDの前半部分と後半部分を破棄するのが一般的です。
PostMDDiffusionFeature では、パラメータ effective_msd_range を使ってフィッティングに用いる範囲を設定することができます。

Tips#

  • 拡散係数の計算後にMSDのプロットを確認するようにしてください。
    拡散係数が低いにもかかわらずシミュレーション時間が不十分な場合などに、MSDの線形関係が現れないことがあります。
    そうなった場合、拡散係数の計算結果に大きな誤差が生じるおそれがあります。

  • stride=100 のように、stride を大きな値に設定することで計算時間を減らすことができます。
    MSDは毎 stride スナップショットごとに計算されます。
    拡散係数は原子の長時間にわたる変位から得られるため、stride の値を大きくしても計算精度にそれほど影響しません。

  • 上で述べたとおり、segment法のほうが精度面で優れていますが、normal法よりも計算時間が多くかかります。

  • パラメータ effective_msd_range を指定することで、MSDの冒頭と末尾の部分を破棄し、線形性の良い部分のみを拡散係数のフィッティングに用いることができます。

Reference#

[1] Pranami, G. & Lamm, M. H. Estimating Error in Diffusion Coefficients Derived from Molecular Dynamics Simulations. J. Chem. Theory Comput. 11, 4586–4592 (2015).