はじめに#

「粘度」は液体の変形に対する抵抗の強さを表す、重要な特徴量です。
PostEMDViscosityFeature
では、グリーン-久保公式に従ってMDトラジェクトリから粘度を評価します。

計算手法#

グリーン–久保公式によると、粘度は次のように表されます。

[eta_{GK} = frac {V} {k_B T} int dt]

(sigma_{alpha beta}) は応力テンソルの非対角成分、 () は応力テンソルの自己相関関数です。

matlantis-features では、 PostEMDViscosityFeature によりグリーン-久保公式に基づく粘性計算を行なうことができます。

PostNEMDViscosityFeature とは異なり、MDシミュレーションの手続きを変更する必要はありません。
したがって、 MDFeature によって得られたMDトラジェクトリをそのまま PostEMDViscosityFeature で用いることができます。

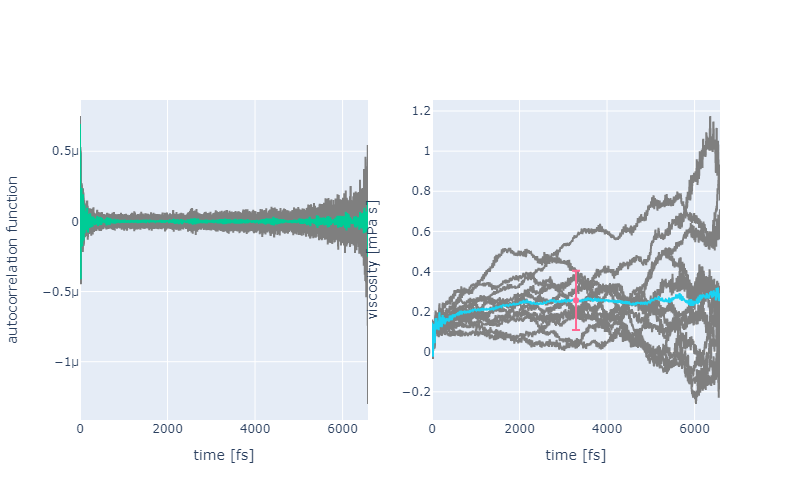
../_images/viscosity_emd.png

応力テンソルの自己相関関数 (左) および粘度 (右)。#

左図では、典型的な応力テンソルの自己相関関数をプロットしています。短時間の相関は大きいため、グラフの序盤では大きな変化が見られます。
一方、長時間の相関はサンプル数が不足するため、グラフの終盤では値がゆらぎます
複数のMDトラジェクトリの平均をとることで、グラフ終盤でみられる変動の影響を抑えることができます(緑線)。

右図ではグリーン–久保公式によって得られた粘度をプロットしています。
粘度は左図の自己相関関数の積分に比例しています。
グレーの線は単一のMDトラジェクトリによる結果を表し、水色の線はすべての結果の平均を表します。
前半で急激に増加し、 (t>2000fs) で安定しプラトーを示しています。
粘度はこのプラトーでの値から評価されるべきです。

PostEMDViscosityFeature では、右図に見られる変動を避けるため、MD全体の半分の時間での粘度の値を取得します。
しかし、あくまでこれは経験的な方法です。より確実に粘度を評価するには、時間と粘度の関係のプロットからプラトーを発見し、その値を見積もる必要があります。

rNEMD法との違い#

matlantis-features では粘度を計算するために、 PostEMDViscosityFeature と PostNEMDViscosityFeature の2つの手法が提供されています。
両者の違いは以下のとおりです。

  • MDシミュレーションの設定:

    PostNEMDViscosityFeature ではrNEMD法により得られたトラジェクトリを入力する必要があります。
    そのため、 RNEMDExtension を用いてMD中に速度交換を行わせるよう設定する必要があります。
    一方で、 PostEMDViscosityFeature ではそのような手続きは必要なく、平衡MDの結果を用いて分析をすることができます。

  • 収束性:

    PostEMDViscosityFeature は PostNEMDViscosityFeature に比べて、収束までに長いシミュレーション時間が必要になります。

Tips#

  • 統計的な平均を取るために、MDの結果をいくつかのセグメントに区切って分析することが推奨されています。具体的な方法については、Examples の Matlantis-features: Viscosity (EMD) をご覧ください。

  • 明確なプラトーが現れていない場合、計算結果が正しくない可能性があります。

  • PostEMDViscosityFeature では、正確な計算結果を得るために長いMDシミュレーション時間が必要になることが多いです。

Reference#

  1. Zhang, Y., Otani, A. & Maginn, E. J. Reliable Viscosity Calculation from Equilibrium Molecular Dynamics Simulations: A Time Decomposition Method. J. Chem. Theory Comput. 11, 3537–3546 (2015).