2025.12.25

機械学習ポテンシャル入門: 材料開発を加速するシミュレーション技術

はじめに

材料科学、化学、そして創薬のR&D現場において、原子・分子レベルのシミュレーションは、物質の性質や反応メカニズムをミクロな視点から解明するための基盤技術として定着しています。しかし、研究開発現場での本格的な活用には、常に「精度」「計算コスト」「汎用性」のトレードオフという壁が立ちはだかっていました。

例えば、第一原理計算は量子力学に基づき高精度な予測が可能ですが、計算コストが極めて高く、スーパーコンピュータを駆使しても「数百原子・数ピコ秒」程度が実用的な限界です。そのため、長時間スケールが必要な現象（界面反応やイオン拡散など）やナノスケール以上のサイズを持つ対象(実在系ナノ粒子触媒など)の計算は困難でした。

一方で、古典力学に基づく分子シミュレーションは、簡易な関数（調和振動子やレナード・ジョーンズ・ポテンシャルなど）を用いることで「数百万原子・数マイクロ秒」の大規模計算が可能ですが、精度や適用範囲はパラメータ（力場）の設計に強く依存します。力場の調整には深い専門知識と試行錯誤が必要で、開発に年単位の時間を要することも珍しくありません。

この長年のジレンマを解消する技術として、現在急速に注目を集めているのが、機械学習ポテンシャル (MLIP: Machine Learning Interatomic Potential) です。本記事では、材料開発の現場を変革しつつあるMLIPの技術的背景について、「アーキテクチャの進化」「学習データの質と多様性」「モデルの検証手法」という3つの観点から、最新の研究動向も交えつつ解説します。

(1) MLIPのアーキテクチャの進化

MLIPは、第一原理計算によって生成された高精度なエネルギーや力を「教師データ」として、ポテンシャルエネルギー曲面を機械学習モデルに学習させた力場です。

具体的には、入力された原子の座標R = {r₁, r₂, …, r_N}と元素種Zから、系の全ポテンシャルエネルギーEおよび各原子に働く力 F_i = – ∇_i Eを機械学習モデルによって推論します。従来の第一原理計算では電子状態計算（SCFサイクル）や、それに基づいたエネルギー勾配 (力)の計算がボトルネックとなっていました。MLIPはこれらの一連のプロセスを機械学習モデルによる「推論」に置き換えることで、第一原理計算並みの精度を維持しつつ、計算速度を数万〜数千万倍に高速化することに成功しています。

本節で見ていく「アーキテクチャ」とは、原子の座標や元素種といった幾何学的な情報を、コンピュータが処理可能な特徴量へと変換し、最終的なエネルギーへと結びつける「機械学習モデルの設計構造」のことを言います。MLIPの発展は、この原子配置をモデルの中でいかに効率的に、かつ物理的要請 (不変性や同変性)を保ちながら表現するかという、技術の進化と共にあります。

記述子ベースのMLIP (初期のアプローチ)

初期の機械学習ポテンシャルは、原子の座標をそのまま学習させるのではなく、各原子を中心としたカットオフ球内の局所的な原子配置を、固定された数式を用いてベクトルに変換し、それをニューラルネットワークに入力するアプローチをとっていました。このニューラルネットワークに入力するベクトルのことを「記述子（Descriptors）」と呼びます。物理法則上、原子のポテンシャルエネルギーは「並進」「回転」「同種原子の置換」によって変化しません。生の座標値をインプットとするのでは満たす事のできないこの「不変性 (Invariance)」を、記述子設計の段階で担保する必要があります。

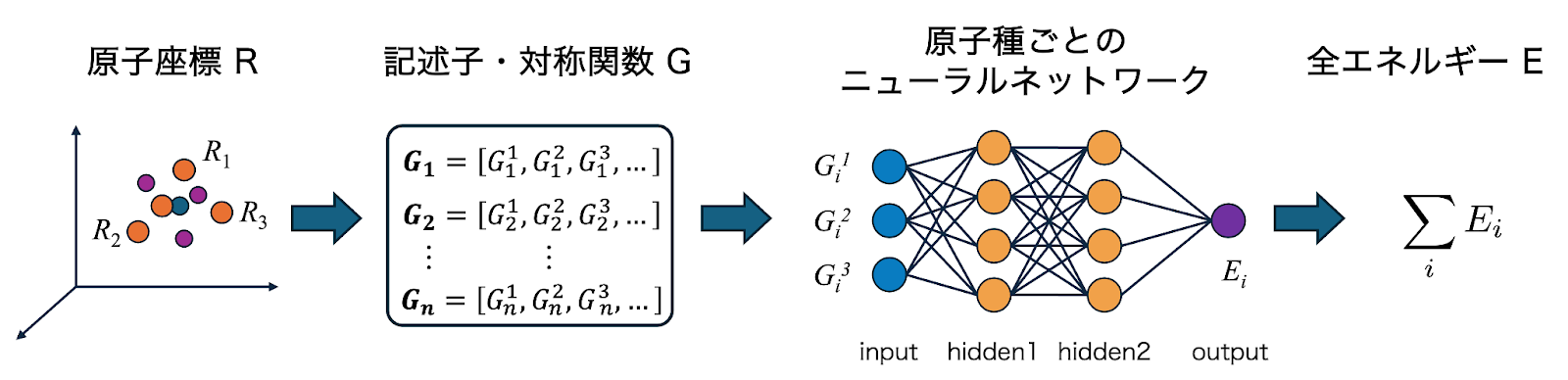
図1: 記述子ベースの機械学習ポテンシャルの概要

この分野でのパイオニア研究として知られるのが、2007年にBehlerとParrinelloが提唱したBehler-Parrinello Neural Network です[1]。彼らは、原子のデカルト座標ではなく、原子間距離や結合角度といった相対的な情報をガウス関数などで表現する原子中心対称関数 (Atom-Centered Symmetry Functions: ACSF) を記述子として採用しました。

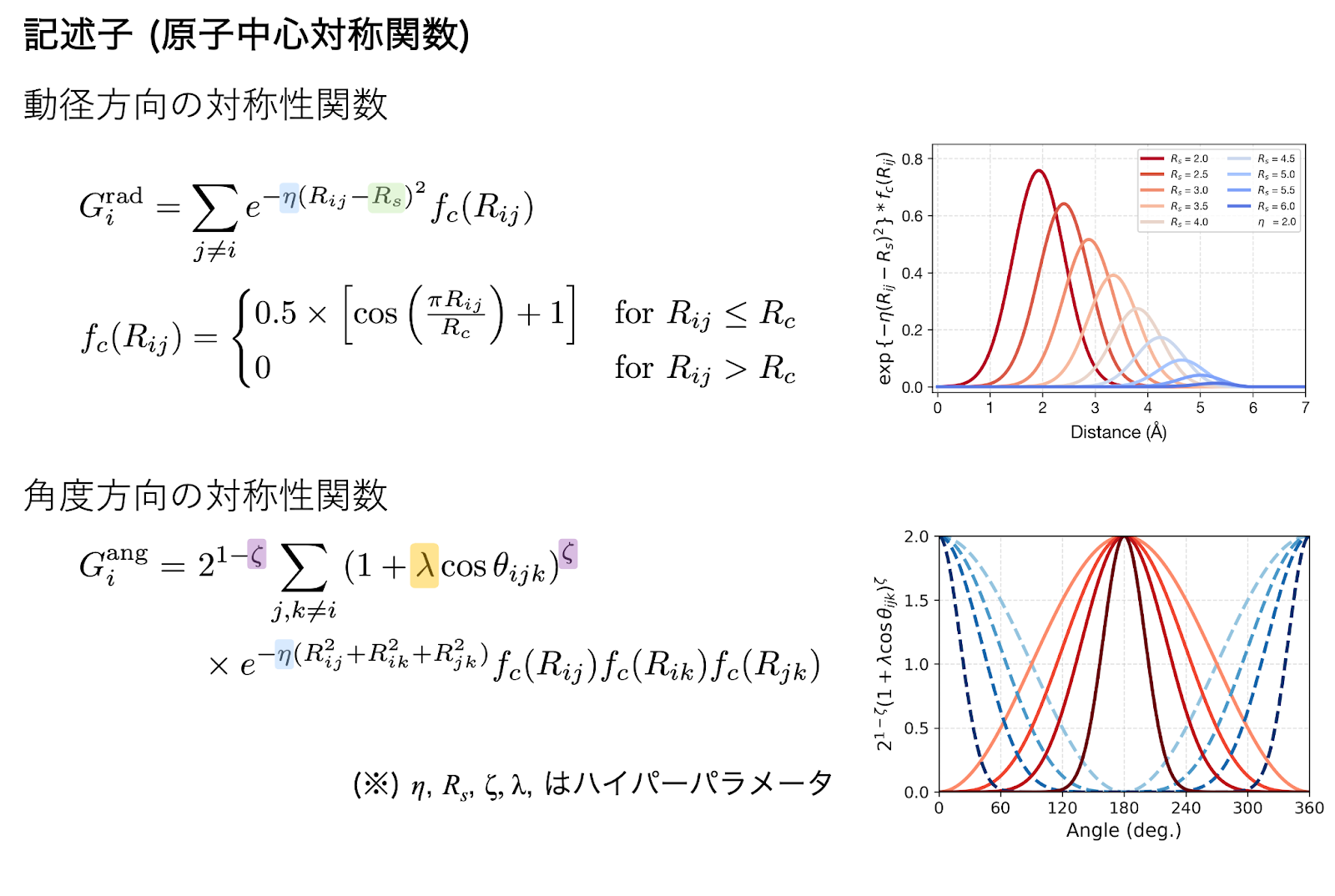
図2: Behler-Parrinello型ニューラルネットワークポテンシャルに使われる記述子関数

また、Bartókらが提唱したSOAP (Smooth Overlap of Atomic Positions) も代表的な記述子の一つです[2]。これは原子密度を球面調和関数で展開し、最終的にその係数の内積をとることで回転不変性を数学的に保証します。

しかし、ハイパーパラメータを手動で調整する必要がある点に加えて、元素種が変数化されていないため、元素の組み合わせごとに個別の記述子を定義しなければならない点が課題となっていました。元素種数が増えると記述子の次元数も組み合わせ論的に増大してしまうため、多元系への拡張は計算コスト観点から現実的ではありませんでした。

グラフニューラルネットワークに基づいたMLIP

現在、特に汎用MLIPにおいてスタンダードとなりつつあるのが、グラフニューラルネットワークです。弊社が提供する汎用原子レベルシミュレータ「Matlantis」のPFPもこの技術を採用しています。

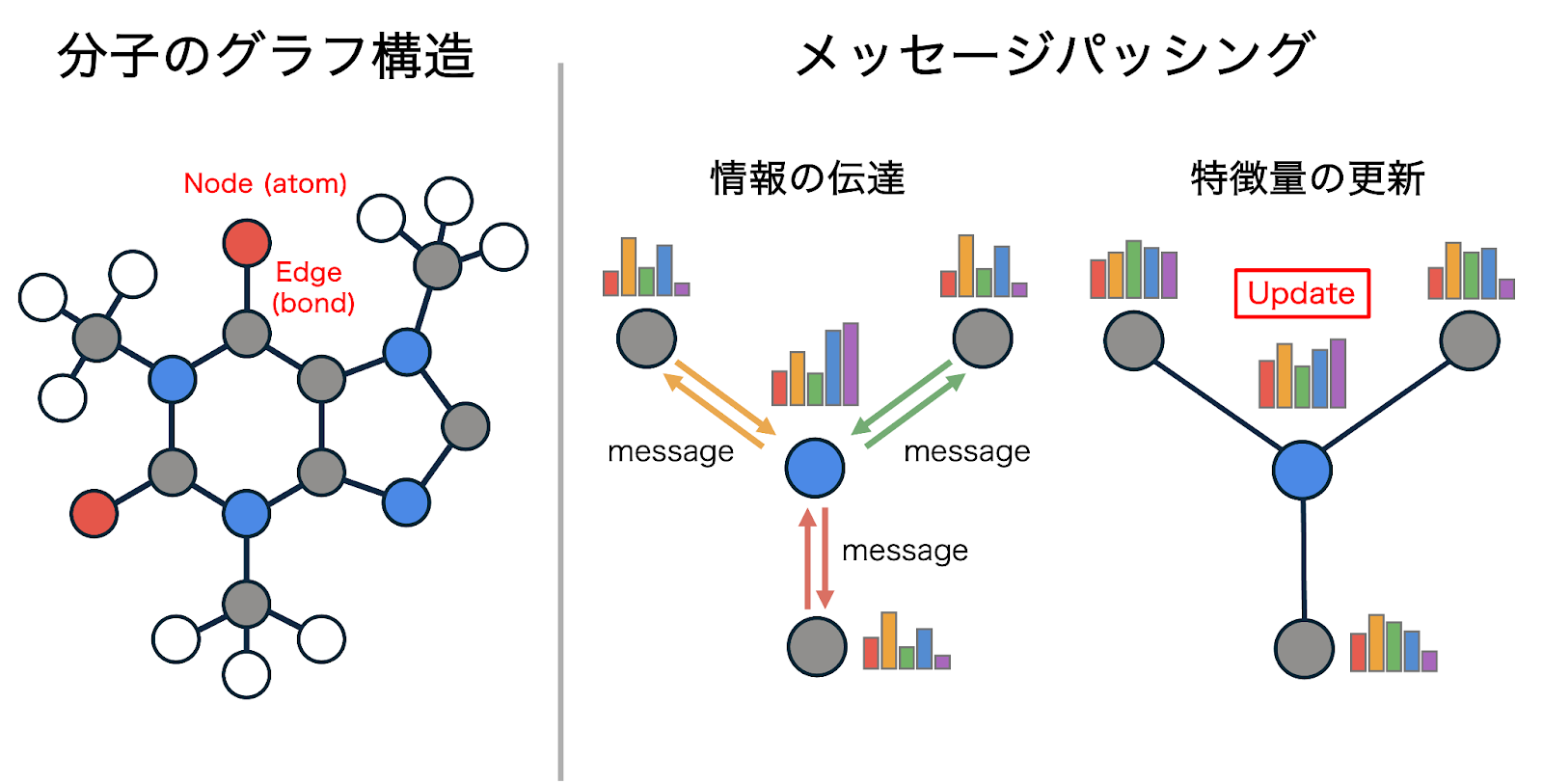
図3: 分子のグラフ表現とメッセージパッシング機構

グラフニューラルネットワークでは、原子を「ノード」、原子間の相互作用（結合）を「エッジ」と見なすグラフ構造で物質を表現します。記述子ベースとの一番の違いは、原子の局所環境を表す特徴量を、人間が手作業で設計するのではなく、モデル自身が訓練プロセスを通じて「埋め込み表現（Embedding）」として学習する点にあります。これにより、機械学習モデルは元素間の化学的な類似性を特徴量空間で効率的に表現することができ、多種類の元素が混在する複雑な系であっても効率的かつ高精度にモデリングすることができます。

また、グラフニューラルネットワークの核となるのが「メッセージパッシング (Message Passing: MP)」と呼ばれるメカニズムです。近接する原子同士が互いに情報（メッセージ）を交換し合い、その情報を集約することで、各原子の埋め込み表現を反復的に更新していく仕組みです。これにより各原子は自身の局所環境だけでなく、より遠くの原子からの情報を間接的に取り込むことが可能となり、系全体の化学的性質や構造特性を反映した表現を獲得することができます。

「不変 (Invariant)」から「同変 (Equivariant)」へ

グラフニューラルネットワークの進化において重要なのが、原子の幾何学的な情報（回転や並進）をどう扱うかというアプローチの違いが挙げられます。具体的には、「不変(Invariant)」と「同変 (Equivariant)」の2つのアプローチに分類することができます [3]。

不変 (Invariant)なメッセージパッシング
初期のグラフニューラルネットワークモデルでは、原子間距離などのスカラー量(座標系を回転させても値が変わらない量)のみをメッセージとしてやり取りしていました。計算はシンプルですが、原子の相対的な方向(=ベクトル)は特徴量として扱わないため、幾何学的な表現力に限界があります。
- 代表例: SchNet (2017)、AIMNet (2019)、DimeNet (2020)など。

同変 (Equivariant)なメッセージパッシング
スカラーだけでなく、ベクトルや高階テンソルといった「同変な特徴量(座標系の回転に応じて自身も回転する量)」もメッセージとして伝搬させます。原子の相対的な向きを特徴量に組み込めるため、不変なMP手法と比較してデータ効率と構造表現能力が大幅に向上します。
- 代表例: PFPの前身であるTeaNet (2019)、NequIP (2021)、Mace (2022)、Allegro (2023)、UMA (2025)など。

(2) 学習データの収集

MLIPの構築において、アーキテクチャの選定以上に重要なのが「学習データの収集」です。実用的で堅牢な汎用モデルを作るためには、単に第一原理計算のデータを大量に集めるだけでは不十分です。広大な化学・構造空間をいかに効率的かつ網羅的にサンプリングするか、データセットの質がMLIPの精度と実用性を決定づけます。

平衡状態に偏ったデータセットの問題

Materials Projectなど、従来から存在している公開データセットでは、エネルギー的に安定な「平衡構造」付近のデータが圧倒的多数を占めていることがあります。Dengら(2024) [4]の研究によると、このような平衡点付近に偏ったデータセットで学習させた汎用MLIP(例えばM3GNet, CHGNet, MACEなど)は、「ポテンシャルの系統的な軟化 (Systematic Softening)」と呼ばれる現象を引き起こします。

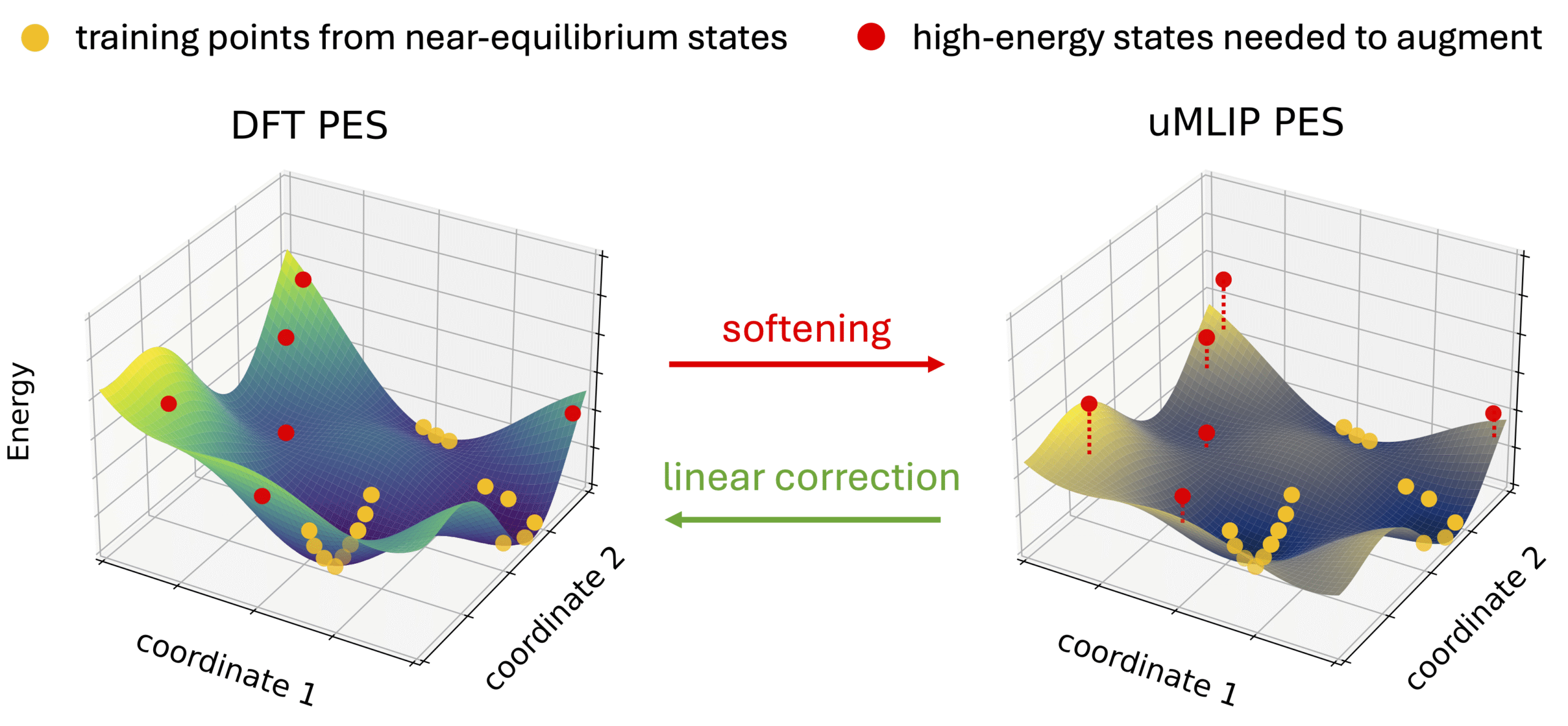
図4: 汎用MLIPの軟化したポテンシャルエネルギー表面 (PES) 。(出典: Deng et al., “Overcoming systematic softening in universal machine learning interatomic potentials by fine-tuning”, licensed under CC BY 4.0)

これはポテンシャルエネルギー曲面の曲率を過小評価してしまい、特に平衡状態から離れた領域において、エネルギーや原子間力を系統的に過小評価してしまう現象で、以下のような問題につながります:

表面・欠陥エネルギーの過小評価
フォノン振動数の過小評価
イオン移動障壁 (バッテリー材料など)の過小評価
高温での分子動力学シミュレーションの破綻

この問題を解決するためには、意図的に非平衡構造（高エネルギー状態）や歪んだ構造を学習データに含めることが不可欠です。実際 Dengらの研究では、わずか数点の高エネルギー構造データを追加学習させるだけで、ポテンシャルの軟化問題が改善することも示されています。

データセットに多様な構造を含めることの重要性

前節で述べたポテンシャルの系統的軟化は、学習データが安定構造付近に集中しすぎていることが主な原因でした。実用的なMLIPを開発するためには、データ量だけでなく、構造空間をバランスよくカバーする「データセットの質と多様性」も重要であることが実証されつつあります。

Kaplanら（2025）[5]によるMatPESの研究が、その好例です。この研究では、約40万構造という比較的小規模なデータセットで学習させたモデルが、約1億件もの構造を含む巨大データセット「OMat24」を用いたモデルと同等、あるいはそれ以上の性能を達成したと報告しました。

なぜ、1/250のデータ量で同等以上の性能が出せたのでしょうか？その鍵を握るのが、データセットがカバーしている「構造空間の領域の広さ」にあります。

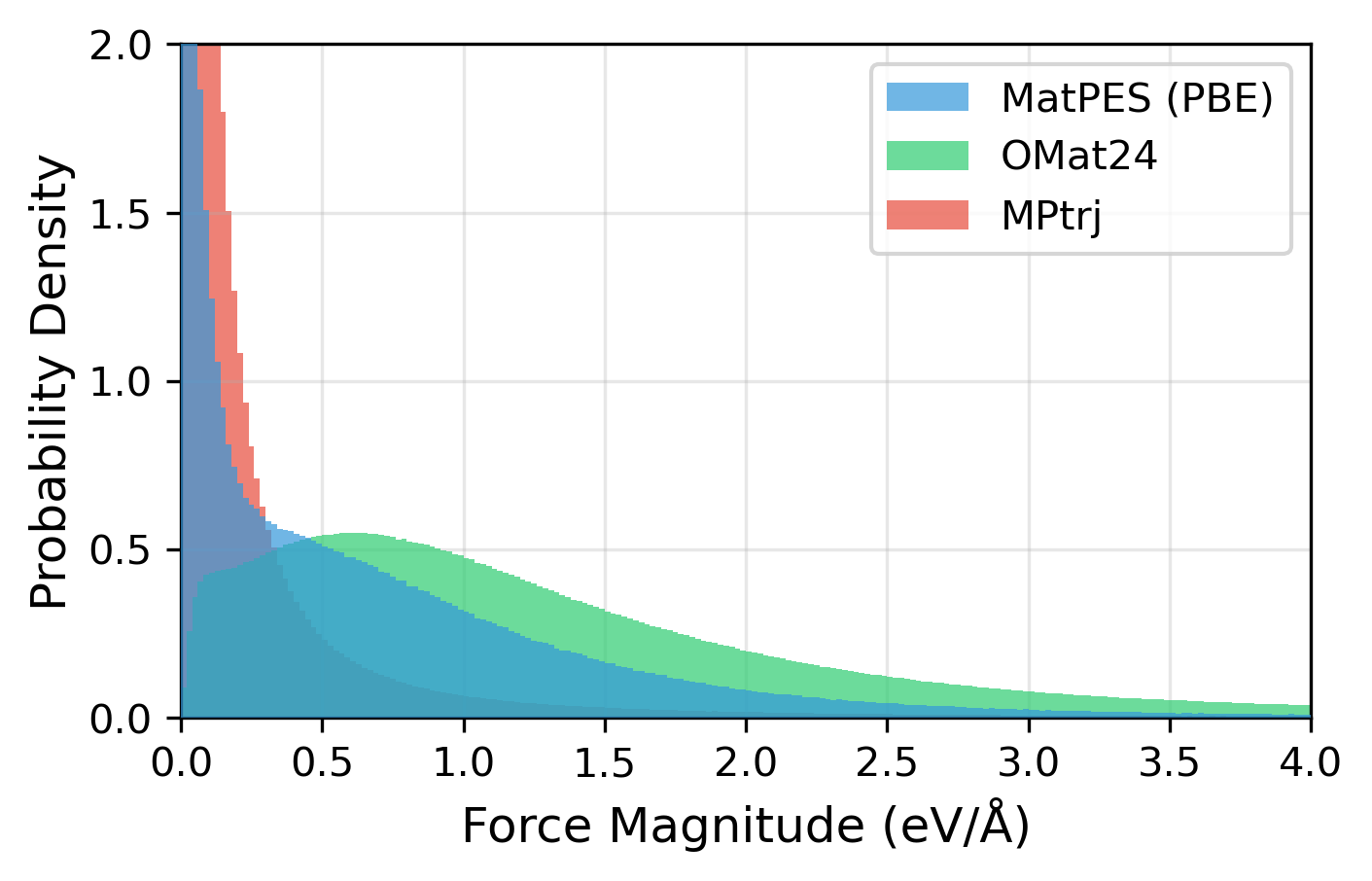
図5: MatPES (PBE) [6], OMat24 [7], MPtrj [8] の各データセットに含まれる構造と力の分布。OMat24は平衡点から離れた力が大きい領域のデータが支配的であるのに対し、MPtrjは平衡点付近の力が小さい領域に集中している。MatPESは両領域をバランスよく網羅しているのが特徴である。Kaplan (2025) Fig2を参考に筆者作成。

MPTrj (Materials Project) のデータセットは構造最適化計算の軌跡データであるため、データの大半がエネルギーの低い平衡点付近に偏っているという問題点があります。一方で、OMat24のデータセットは第一原理分子動力学データを大量に含み、高エネルギー状態のデータは豊富だが、平衡状態付近のサンプリング密度が相対的に低いという問題点がありました。

これに対してMatPESでは、平衡点付近と、そこから適度に離れた非平衡状態のバランスを重視してデータセットを構築しています。また「2DIRECT」と呼ばれるサンプリング手法を用いて、構造的・化学的に重複の少ないデータを厳選しています。その結果、約40万構造という比較的小規模なデータセットながら、約1億件もの構造を含むOMat24で学習させたモデルと同等以上の性能を達成しました。

この報告は、似たような安定構造を無数に学習させるよりも、モデルにとって未知の領域や物理的に重要な領域をバランスよく学習させる方が、計算コスト対効果（データ効率）が高いことを示唆しています。

構造多様性を確保するためのサンプリング戦略

それでは具体的にどのようにすれば「多様性」をデータセットに含めることができるのでしょうか? Kulichenkoら (2024) [9]がChemical Reviewに発表した総説では、構造多様性を確保するために以下のようなサンプリング戦略が提案されています。

能動学習 (Active Learning): モデルの予測不確実性が高い領域を重点的に計算・学習させることで、人間のバイアスを排除しつつ、最小限のコストでデータの多様性を最大化する。
レアイベント探索手法: 通常のMDでは到達困難な領域を探索するために、メタダイナミクスや、モデルの不確実性をバイアスとして利用する不確実性駆動ダイナミクス、遷移状態サンプリングなどを活用する。

Matlantisにおけるデータセット構築

ここまでに述べた「非平衡・不安定構造データの重要性」は、2024-2025年の最新研究によって再評価されたものですが、この戦略をいち早く実践して実用化した例がMatlantisに搭載されているPFPです。

2022年にNature Communicationsで発表されたPFPの論文 [10]において、開発チームは「既存の安定構造を集めるのではなく、モデルの頑健性と汎用性を高めるために、不安定な構造を積極的に収集した（We aggressively gathered a dataset containing unstable structures）」といった戦略を示しています。

具体的には、以下のような不安定な状態を意図的に網羅するアプローチをPFP開発時点(2021年)で既に実践しています [11, 12]。

結晶構造内の元素を不規則に置換する
多様な元素が共存する無秩序な構造を作る
温度や密度を大きく変化させて、平衡から離れた状態を作り出す
高温分子動力学シミュレーションや能動学習を駆使して、広範な化学空間をカバーする

このような「データ量だけでなく質（多様性）も重視する」というデータセット構築戦略こそが、PFPが未知の材料や複雑な化学反応に対しても高い汎用性と堅牢性を発揮できる理由だと言えます。

また、PFPのデータセットは2021年にMatlantisのサービスを開始して以来、実際の材料開発に携わるお客様のフィードバックを得ながら継続的にアップデートし続けている点も、他の公開データセットと比較した際の強みの一つとなっています。

(3) MLIPの検証方法

モデルを作成した後、その正しさをどう検証するかも重要な課題です。従来は、静的な構造に対するエネルギーや力の予測誤差（MAEなど）が重視されてきましたが、これだけではシミュレーション時の不自然な挙動（構造破綻や異常な物理挙動）を防げないケースがあります。

こうした課題に対し、近年では「静的な誤差」よりも「シミュレーション結果や物性値」を重視する検証手法が主流になりつつあります。例えば、MLIP Arena (2025) [13]やCHIPS-FF (2025) [14]といった最新のベンチマークは、共通して「物理量の妥当性」を評価軸に据えています。

MLIP Arena: 単に誤差ベースの回帰指標に合わせるだけでなく、エネルギー保存則が守られているか、原子間距離が極端に近づいた際にポテンシャル曲線が不自然な挙動を示さないか、といった物理モデルとしての素性の良さもチェックしています。また極端な高温・高圧条件下でシミュレーションが破綻しないかというストレステストなどもベンチマークとしています。
CHIPS-FF: 弾性率、フォノンバンド構造、欠陥形成エネルギーといった、材料開発の現場で必要となる具体的な物性値の再現性を評価しています。

MatlantisのPFPにおいても、単にエネルギー・力の検証のみにとどまらず、様々な材料物性について多角的な検証を経て、物理的に妥当な汎用力場として提供されています。PFPの検証結果の一部は以下のページでも公開しておりますのでぜひご覧ください。